[Algorithm] 벨만-포드 알고리즘

[Algorithm] 벨만포드 알고리즘

벨만 포드 알고리즘는 최소 비용을 구하는 알고리즘이다. 하나의 출발점에서 모든 도착지까지의 걸리는 최소 비용을 구한다는 점에서 다익스트라와 비슷하다.
다익스트라 알고리즘은 음의 가중치를 허용하지 않는다.
그러나 벨만포드에서는 음의 가중치를 허용한다. 그렇지만 음의 사이클이 존재할 경우, 알고리즘은 제대로 동작하지 않으며 최단 경로를 구할 수 없다.

벨만포드 알고리즘 (Bellman-Ford) 특징

벨만 포드 알고리즘은 모든 경우의 수를 다 탐색해 가면서 최소 비용을 찾는다. 따라서 다익스트라와는 다르게 그리디하게 작동하지 않는다.

벨만포드는 모든 간선들을 탐색하면서, 간선이 잇는 출발 정점이 한번이라도 계산된 정점이라면 해당 간선이 잇는 정점의 거리를 비교해서 업데이트한다. 그리고 이 과정을 (정점개수-1) 만큼 반복한다.

또한, 음의 사이클이 존재하는지 확인할 수 있다. ( 정상적인 그래프라면 V-1번 탐색한 후 또 한번 탐색을 진행하더라도 최소비용이 변하는 정점이 발생하지 않는다. 그러나 음의 사이클이 존재할 경우, 최소 비용이 변하게 되므로 이 점에서 음의 사이클의 존재여부를 확인할 수 있다.)

이 외에도 동작원리가 궁금하다면 최단 경로 알고리즘 “최단 경로 알고리즘 정리”을 정리해둔 글로 가면 자세한 동작 원리를 확인해 볼 수 있다.

구현 방법

동작 과정

1. 출발 노드를 설정한다.
2. 최단 거리 테이블을 초기화한다.
3. 간선 E개를 전부 하나씩 확인한다.
4. 각 간선을 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블을 갱신한다. (3,4번을 V-1번 반복한다.)

음수 사이클의 여부를 확인하고 싶다면, 3번 과정을 한번 더 수행하면 된다. 이때 최단 거리 테이블이 갱신되면, 음의 사이클이 존재하는 것이다.

소스코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.StringTokenizer;

class Edges{
    int start;
    int end;
    int cost;
    public Edges(int start, int end, int cost){
        this.cost=cost;
        this.end=end;
        this.start=start;
    }
}
public class BellmanFord {
    static final int INF = Integer.MAX_VALUE;
    static ArrayList<Edges> graph;
    static int N;
    static int M;
    static int[] dist;
    public static boolean Bellmanford(int start){
        Arrays.fill(dist,INF);
        dist[start]=0;
        //정점의 개수만큼 반복
        for(int i=0;i<N;i++){
            //간선의 개수만큼 반복
            for(int j=0;j<M;j++){
                Edges nowEdge = graph.get(j);   //현재 간선
                //현재 간선의 들어오는 정점에 대해 비교
                if(dist[nowEdge.start]!=INF && dist[nowEdge.end]>dist[nowEdge.start]+ nowEdge.cost)
                    dist[nowEdge.end]=dist[nowEdge.start]+ nowEdge.cost; //dist 값이 현재 노드를 거쳐가는 것이 더 작다면 dist 값을 변경한다. 다익스트라 알고리즘과 비슷하다.
            }
        }
        //음수 가중치 확인
        //모든 간선을 한번 더 살펴보면서 dist 값을 확인한다. 만약 값이 더 작아진다면 음수 사이클 존재한다.
        for(int i=0;i<M;i++){
            Edges nowEdge = graph.get(i);   //현재 간선
            //현재 간선의 들어오는 정점에 대해 비교 -> 더 작은 값 생기면 음수 사이클 존재함
            if(dist[nowEdge.start]!=INF&&dist[nowEdge.end]>dist[nowEdge.start]+ nowEdge.cost) {
                System.out.println("음수 사이클 존재");
                return false;
            }
        }
        //출력
        for(int i=0;i<dist.length;i++){
            if(dist[i]==INF) System.out.print("INF ");
            else System.out.print(dist[i]+" ");
        }
        return true;

    }
    public static void main(String[]args)throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        System.out.print("정점의 개수, 간선의 개수 입력>>");
        StringTokenizer st = new StringTokenizer(br.readLine());
        N = Integer.parseInt(st.nextToken());
        M = Integer.parseInt(st.nextToken());
        dist = new int[N+1];
        graph = new ArrayList<>();
        for(int i=0;i<M;i++){
            st = new StringTokenizer(br.readLine());
            int start = Integer.parseInt(st.nextToken());
            int end = Integer.parseInt(st.nextToken());
            int cost = Integer.parseInt(st.nextToken());
            graph.add(new Edges(start,end,cost));
        }
        Bellmanford(4);

    }
}

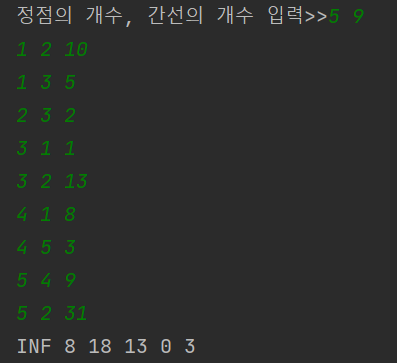
실행 결과는 다음과 같다. 음수 사이클이 있는 그래프를 입력할 경우, 음수 사이클이 존재함을 알 수 있다.

Reference

• Do it! 알고리즘 코딩 테스트 자바 편 (김종관 저, 이지스퍼블리싱)
• [알고리즘/Java] 벨만-포드(Bellman-Ford) 알고리즘, suk13574