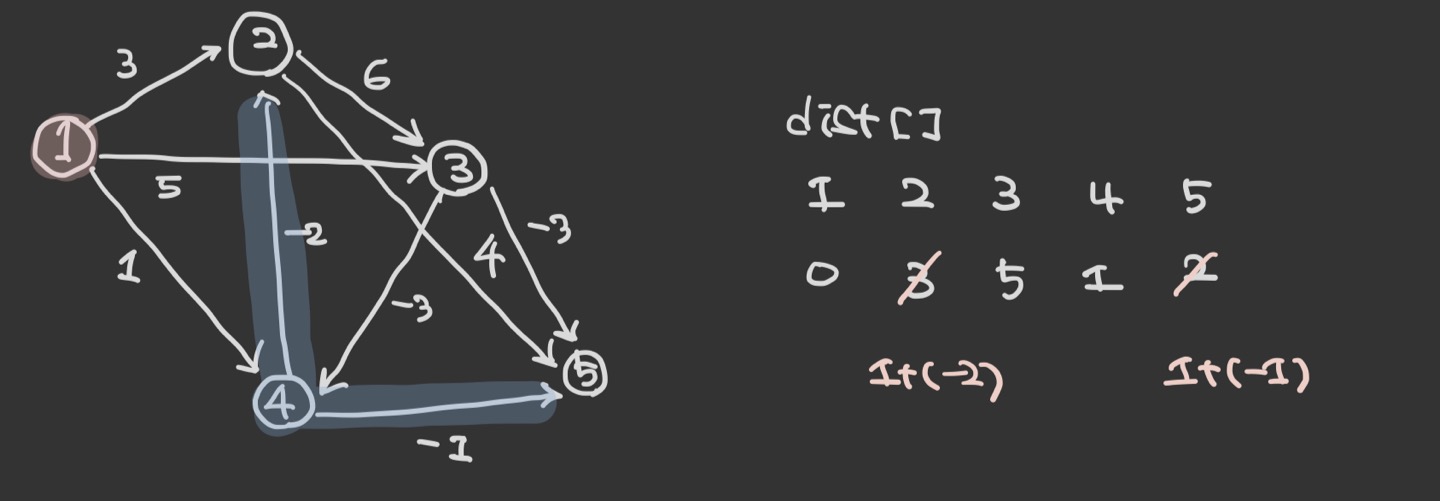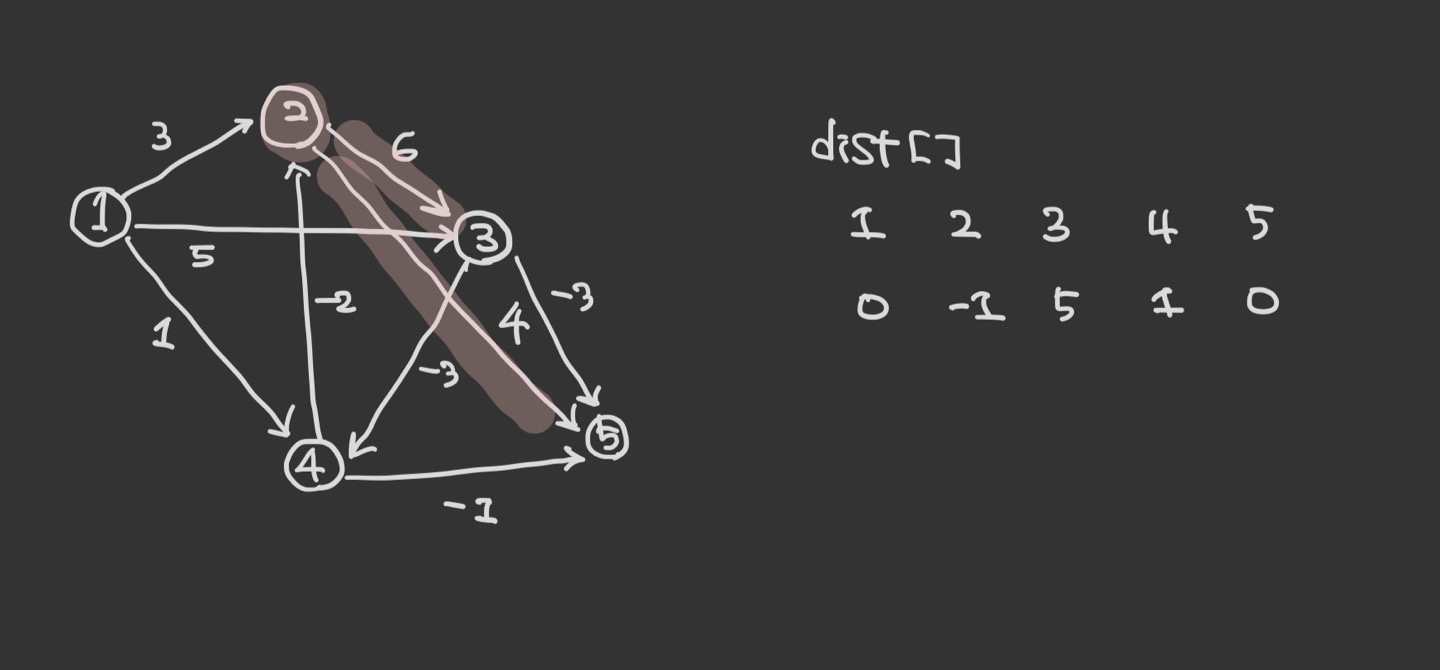[Algorithm] 최단 경로 알고리즘 (다익스트라, 플로이드 워셜, 벨만 포드 )
최단 경로 알고리즘
최단 거리 알고리즘이란, 그래프 상에서 노드 간의 탐색 비용을 최소화하는 알고리즘이다. 즉, 가중 그래프에서 간선의 가중치 합이 최소가 되는 경로를 찾는 문제이다.
최단 경로 문제
최단 경로 문제는 다음과 같이 다양한 문제 상황이 주어진다.
- 단일 출발 (single-source) 최단 경로 : 어떤 하나의 정점에서 출발하여 나머지 모든 정점 까지의 최단 경로를 찾는 문제 ( )
- 단일 도착 (single-destination) 최단 경로 : 모든 정점에서 출발하여 어떤 하나의 정점까지의 최단 경로를 찾는 문제로 그래프 내의 간선들을 뒤집으면 단일 출발 최단거리 문제로 바뀔 수 있다.
- 단일 쌍 (single-pair) 최단 경로 : 단일 정점에서 다른 정점으로 가는 최단 경로 문제
- 전체 쌍(all-pair) 최단 경로 : 그래프 내의 모든 정점 쌍들의 최단 경로를 구하는 문제
주요 알고리즘
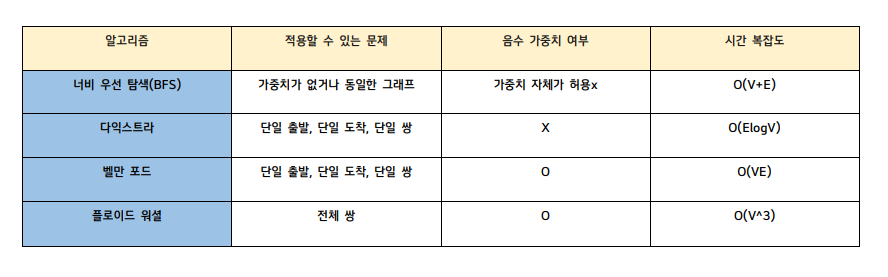
- 다익스트라(Dijkstra) : 음이 아닌 가중 그래프에서의 단일 쌍, 단일 출발, 단일 도착 최단 경로 문제
- 벨만-포드(Bellman-Ford-Moore) : 가중 그래프에서의 단일 쌍, 단일 출발, 단일 도착 최단 경로 문제
- 플로이드 워셜(Floyd-Warshall) : 전체 쌍 최단 경로 문제
- BFS(완전 탐색) : 가중치가 없거나 모든 가중치가 동일한 그래프에서 최단 경로를 구하는 경우 가장 빠름
다익스트라 알고리즘 (Dijkstra)
그래프에 여러개의 노드가 있을 떼, 특정한 노드에서 출발하여 다른 노드로 가는 각각의 최단 경로를 구해주는 알고리즘이며 음의 간선이 없어야 한다는 것이 특징이다. 이는 단일 출발, 단일 도착, 단일 쌍 유형을 해결하는데 적용할 수 있다.
매번 그 순간에 가장 비용이 적은 노드를 선택해서 임의의 과정을 반복하므로, 그리디 알고리즘으로 분류된다. 즉, 다익스트라 알고리즘은 주어진 그래프에서 Greedy 기반으로 최적의 경로를 탐색하는 알고리즘이라고 한다.
- Greedy? : 탐욕 알고리즘으로 매 주어진 상황에서 가장 좋은 경로를 선택함으로써 만들어가는 탐색 방법이다.
또한 현실 세계의 길(간선)은 음의 값을 가지지 않으므로, GPS 소프트웨어의 기본 알고리즘으로 자주 사용된다.
그렇다면 왜 다익스트라 알고리즘은 음의 가중치를 허용하지 않을까? 그 이유는 그리디를 통해 최단 경로라고 여겨진 경로 비용을 DP 테이블에 저장한 뒤, 재방문하지 않는데, 만약 음의 가중치가 있다면 이러한 규칙이 어긋날 수도 있기 때문이다. 따라서 음의 가중치가 있을 경우 플로이드 워셜이나 벨만 포드 알고리즘을 이용해 최단 경로를 구하면 된다.
또한 큐가 아닌 우선순위 큐(힙)으로 더 작은 가중치를 가진 간선을 먼저 탐색하는 방식으로 구현하면 수행시간을 더 줄일 수 있다.
다익스트라 동작 원리
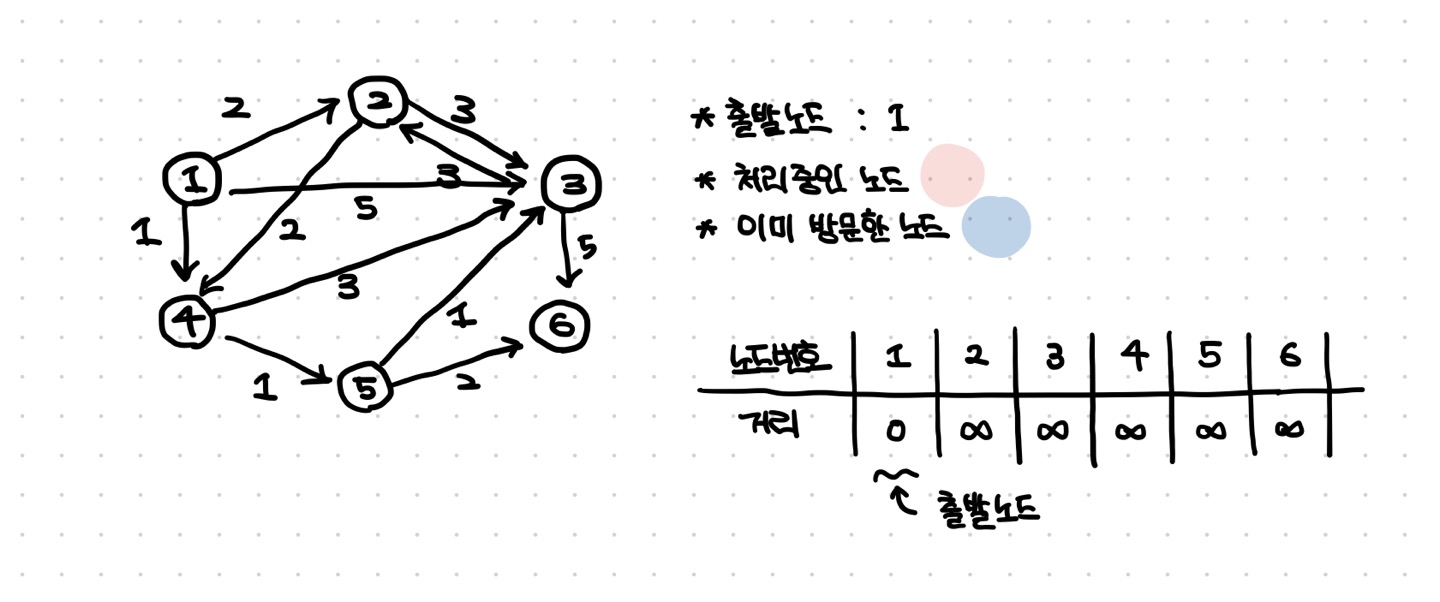
- 출발 노드를 설정한다.
- 최단 거리 테이블을 초기화 한다.(1차원 배열)
- 방문하지 않은 노드 중에서 최단 거리 테이블에 저장된 거리가 가장 짧은 노드를 선택한다. (Greedy)
- 해당 노드를 거쳐서 다른 노드로 가는 비용을 계산해 최단 거리 테이블을 갱신한다.
- 위 과정에서 3번과 4번을 반복한다.
최단 거리 테이블은 각 노드에 대한 현재까지의 최단 거리 정보를 가지고 있다.
동작과정 살펴보기
- 출발 노드를 선정한다.
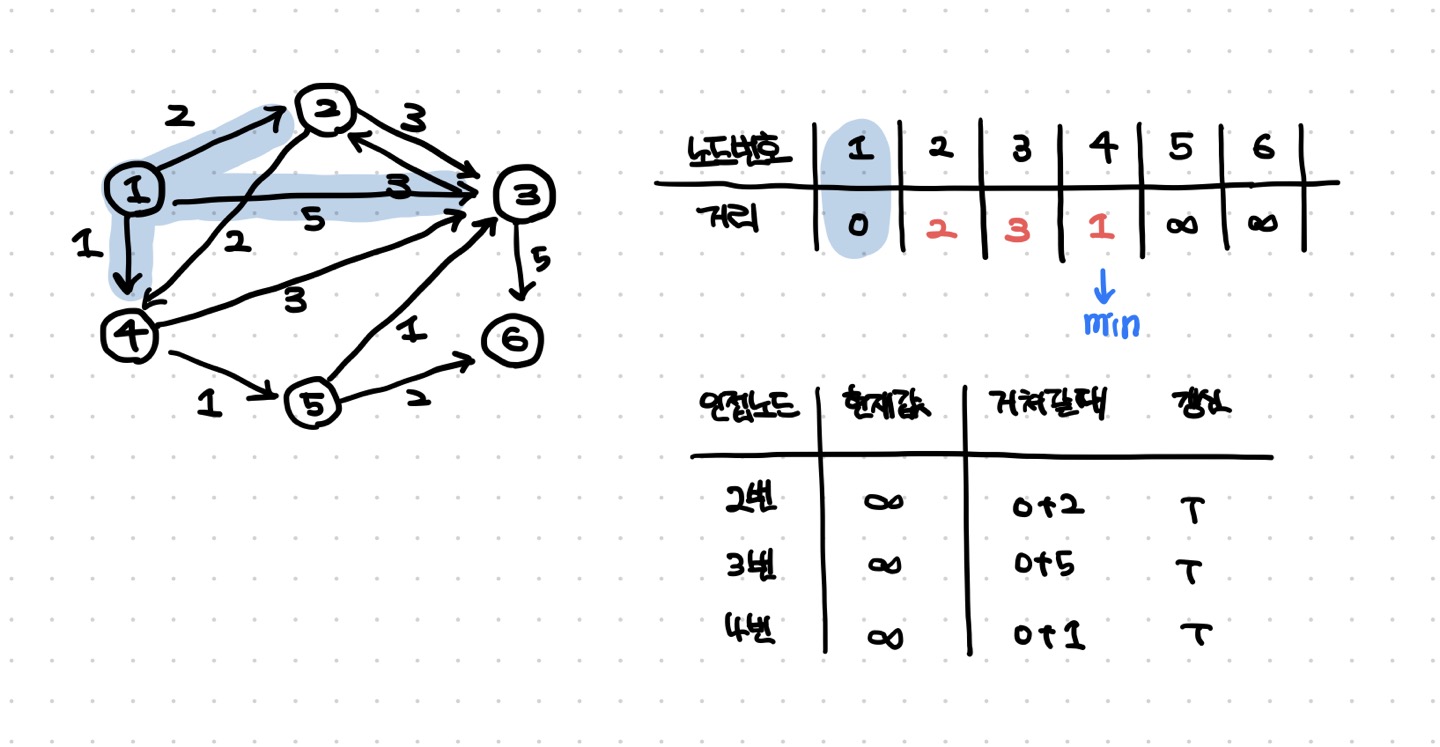
- 방문하지 않은 노드중에서 (최단 거리 테이블에 저장된) 거리가 가장 짧은 노드인 1번을 처리한다. ( 1번에서 이동할 수 있는, 방문하지 않은 인접 노드 :2,3,4번)
- 현재 테이블에 저장된 값보다 1번 노드를 거쳐서 가는 경로가 더 짧으면 값을 갱신한다.
- 또한 한번 방문 처리가 된 노드는 출발 노드로부터의 최단 거리가 확정되어 테이블에 저장된 값을 변경할 수 없다. ( 이런 특성 때문에 그리디 알고리즘으로 최적해를 구할 수 있다. )
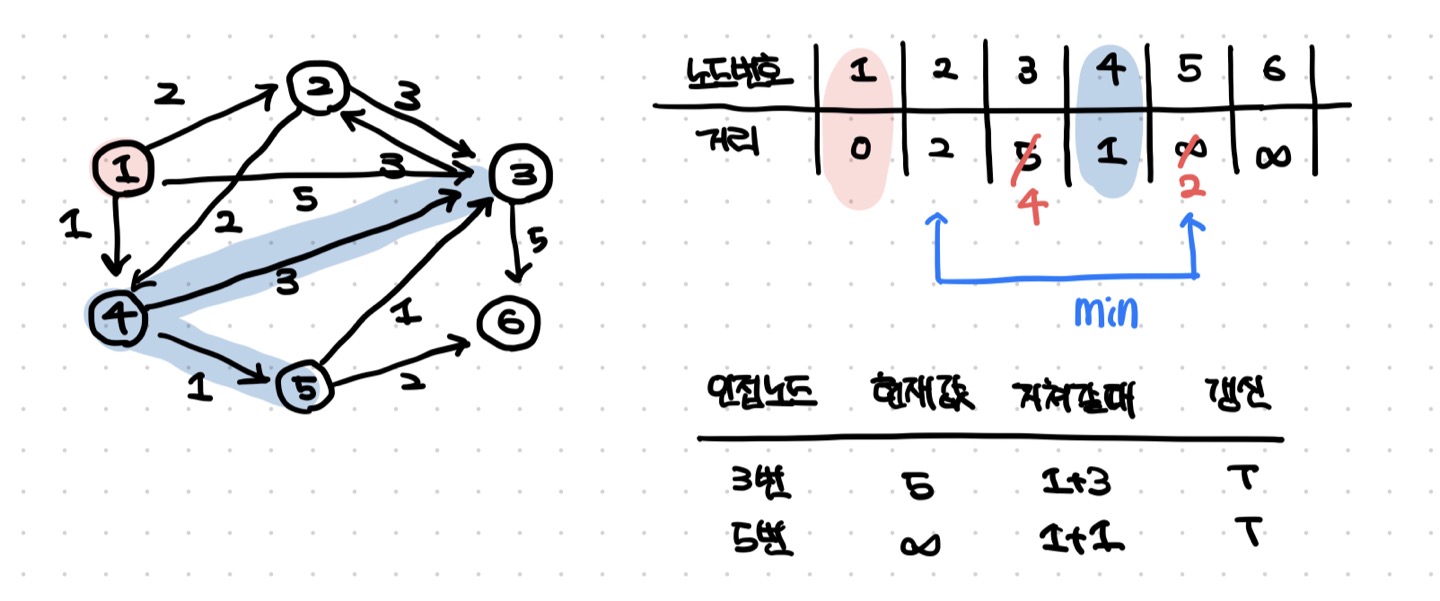
- 방문하지 않은 노드 중에서 최단 거리 테이블에 저장된 거리가 가장 짧은 노드인 4번을 처리한다.
- 4번에서 이동할 수 있는, 방문하지 않은 인접 노드 :3,5번 노드
- 현재 테이블에 저장된 값보다 4번 노드를 거쳐서 가는 경로가 더 짧으면 값을 갱신한다.
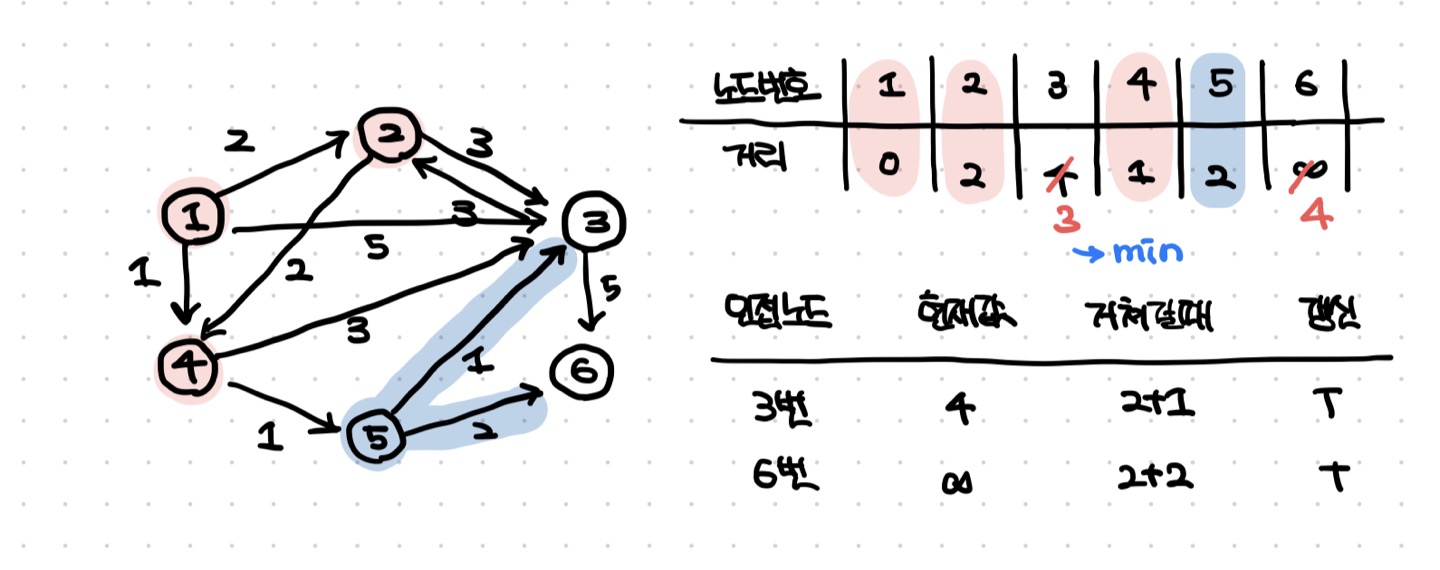
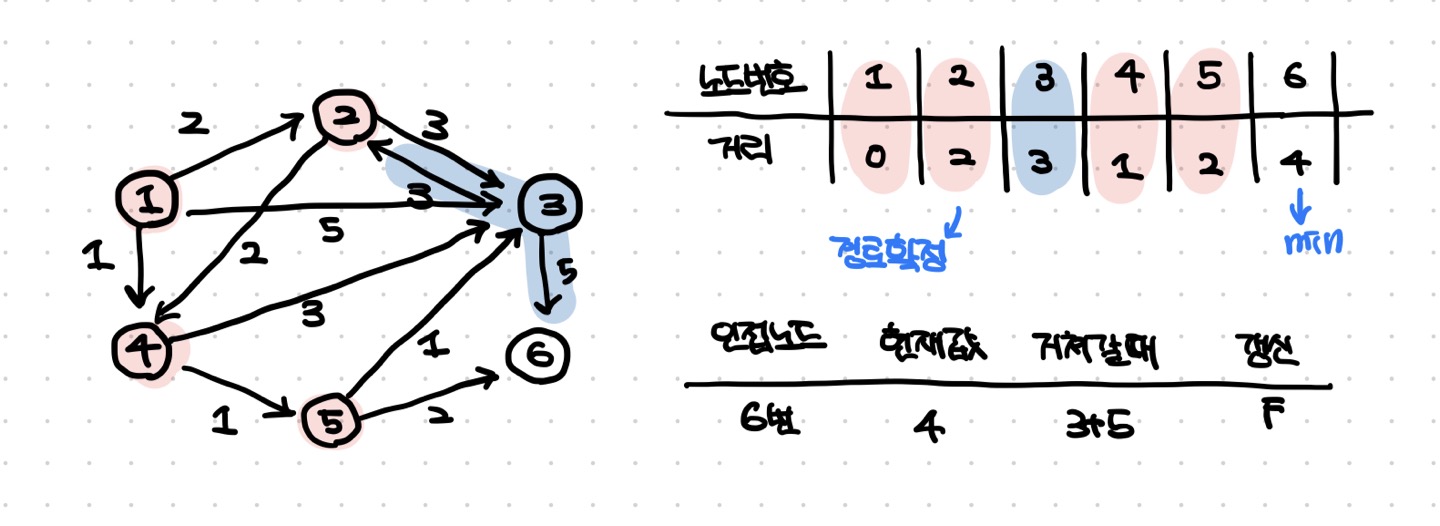
- 방문하지 않은 노드 중에서 최단 거리 테이블에 저장된 거리가 가장 짧은 노드인 2번과 5번 중에 2번을 처리한다.
- 4번은 방문한 적이 있기 때문에 출발 노드로부터의 최단 거리가 확정되어 값을 바꿀 수 없다.
- 현재 테이블에 저장된 값보다 2번 노드를 거쳐서 가는 경로가 더 짧으면 값을 갱신한다.
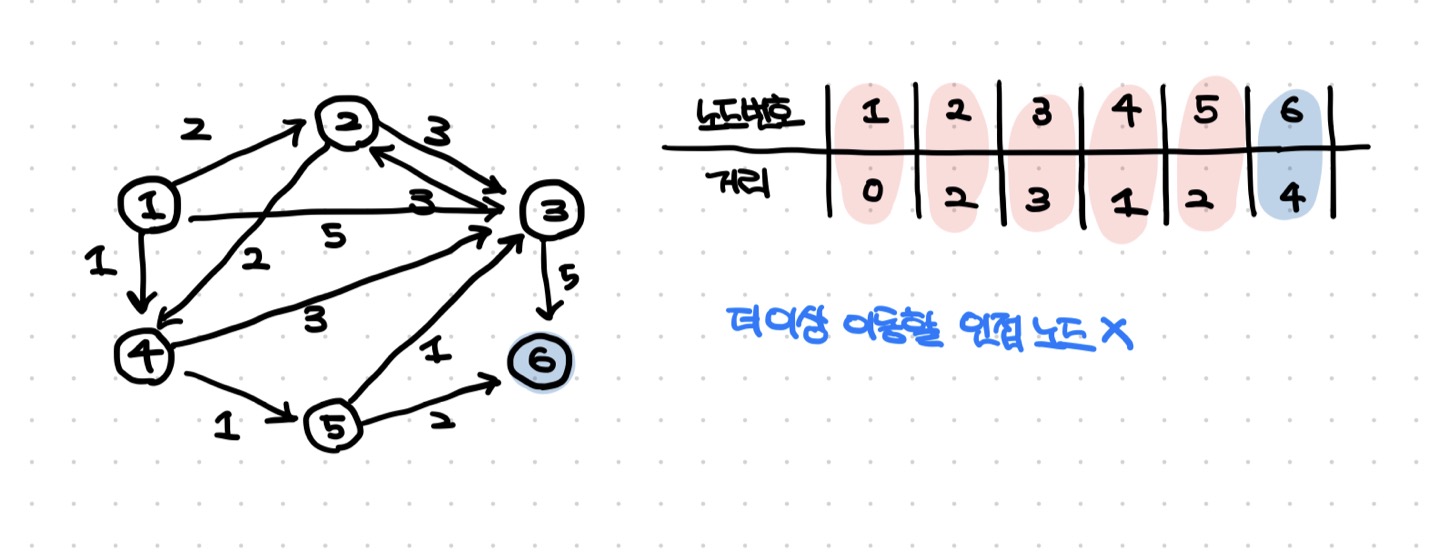
- 이 과정을 계속 반복한다.
다익스트라 알고리즘 정리
- 그리디 알고리즘 : 매 상황에서 방문하지 않고, 가장 비용이 적은 노드를 선택해 임의의 과정을 반복한다.
- 단계를 거치며 한번 처리된 노드의 최단 거리는 확정되어 더 이상 바뀌지 않는다. ( 한 단계당 하나의 노드에 대한 최단 거리를 확실히 찾는 것으로 이해할 수 있다. 따라서 그리디 알고리즘으로 최적해를 보장할 수 있다. )
- 이렇게 다익스트라 알고리즘을 수행하면, 테이블에 각 노드까지의 최단 거리 정보가 저장된다.
벨만 포드 알고리즘 (Bellman Ford)
가중 유형 그래프 상에서 특정 한 노드로부터 다른 노드까지의 최단 경로를 구하는 알고리즘이다. 다익스트라 알고리즘의 한계(간선이 음수 가중치를 가지는 경우 경로를 구할 수 없음)을 개선하기 위해 등장했다. 단일 출발, 단일 도착, 단일쌍 유형을 음수 가중치를 가지는 그래프에서 효율적으로 해결하는데 적용할 수 있다.
벨만 포드 알고리즘은 가중치가 음수인 간선이 존재하는 경우에도 올바르게 동작한다. 그러나 negative cycle을 가진다면 올바르게 동작하지 않으며, 벨만 포드 알고리즘의 성질을 이용하여 negative cycle에 대한 검출을 진행할 수 있다.
벨만 포드는 다익스트라와 동일하지만 간선의 가중치가 음일 때도 최소 비용을 구할 수 있다는 차이점이 존재한다. 그리고 다익스트라보다 시간복잡도가 늘어나는데, 그리디하게 최소 비용 경로를 찾아가는 다익스트라와 달리, 벨만 포드는 모든 경우의 수를 고려하는 동적계획법이 사용되기 때문이다. ( 매 단계마다 모든 간선을 전부 확인하는 것이다. 다익스트라는 출발 노드에서만 연결된 노드를 반복적으로 탐색하며 다른 모든 노드까지의 최소 거리를 구한다. 그러나 벨만 포드는 모든 노드가 한번씩 출발점이 되어 다른 노드까지의 최소 비용을 구한다. )
벨만 포드 동작 원리
음의 사이클이 없고, 정점이 V개인 그래프에서, 한 정점에서 출발한 다른 정점 까지의 최단경로는 많아봐야 V-1개의 간선을 지난다. 모든 정점에 대해 V-1번의 반복을 통해 가능한 모든 경로를 탐색하여 정확한 답을 낸다.
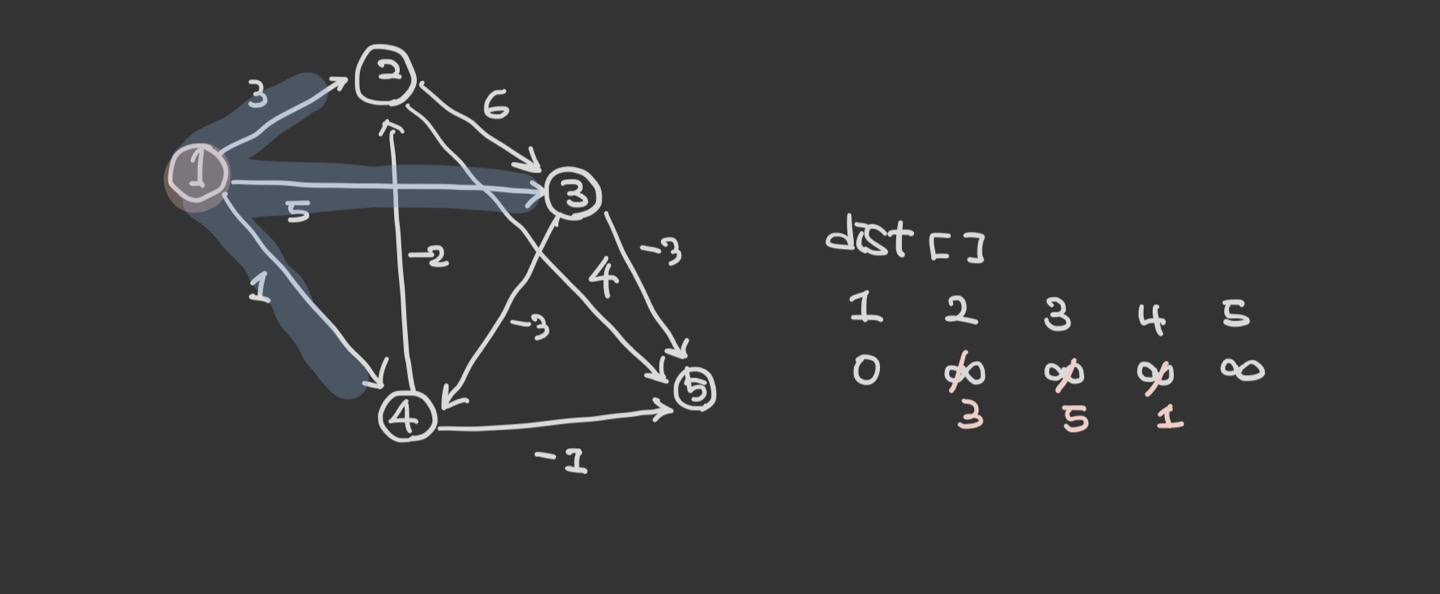
동작 과정 살펴보기
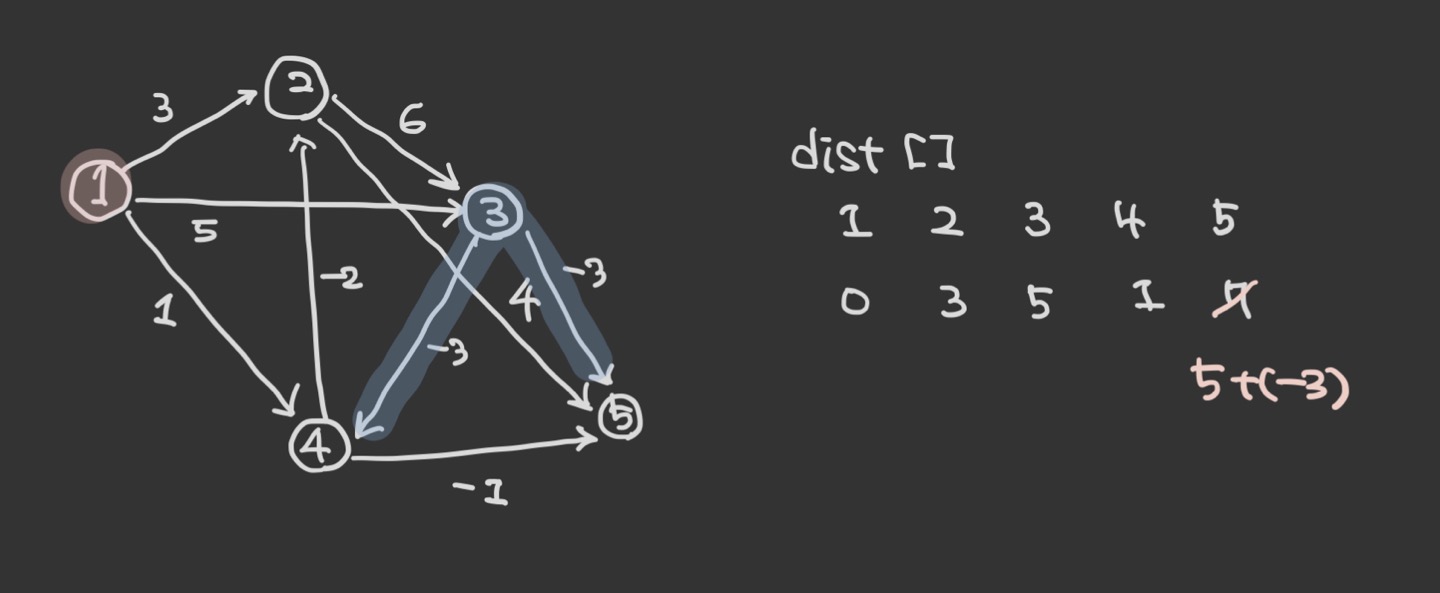
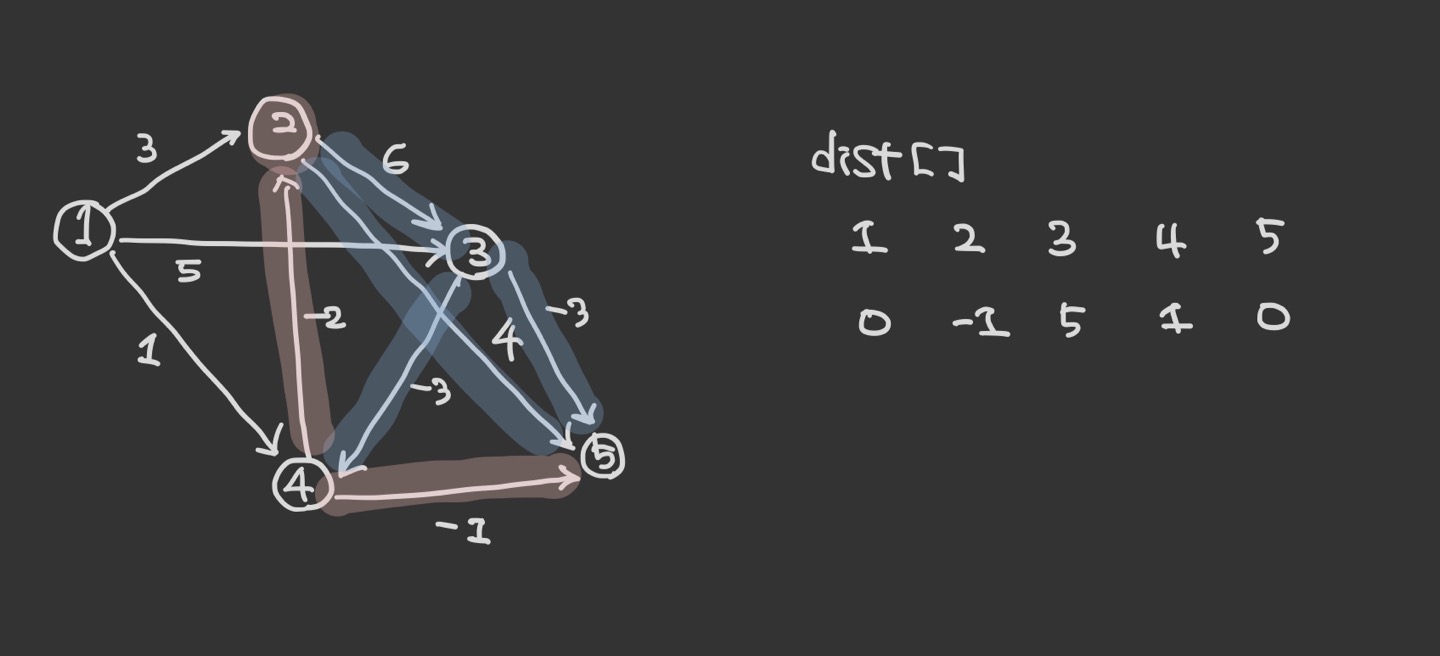
첫번째 반복은 1번 노드에 대해 시작한다. 각 간선을 탐색하는 순서는 상관없다. 값을 갱신하는 것은 위의 다익스트라 알고리즘과 비슷하다.
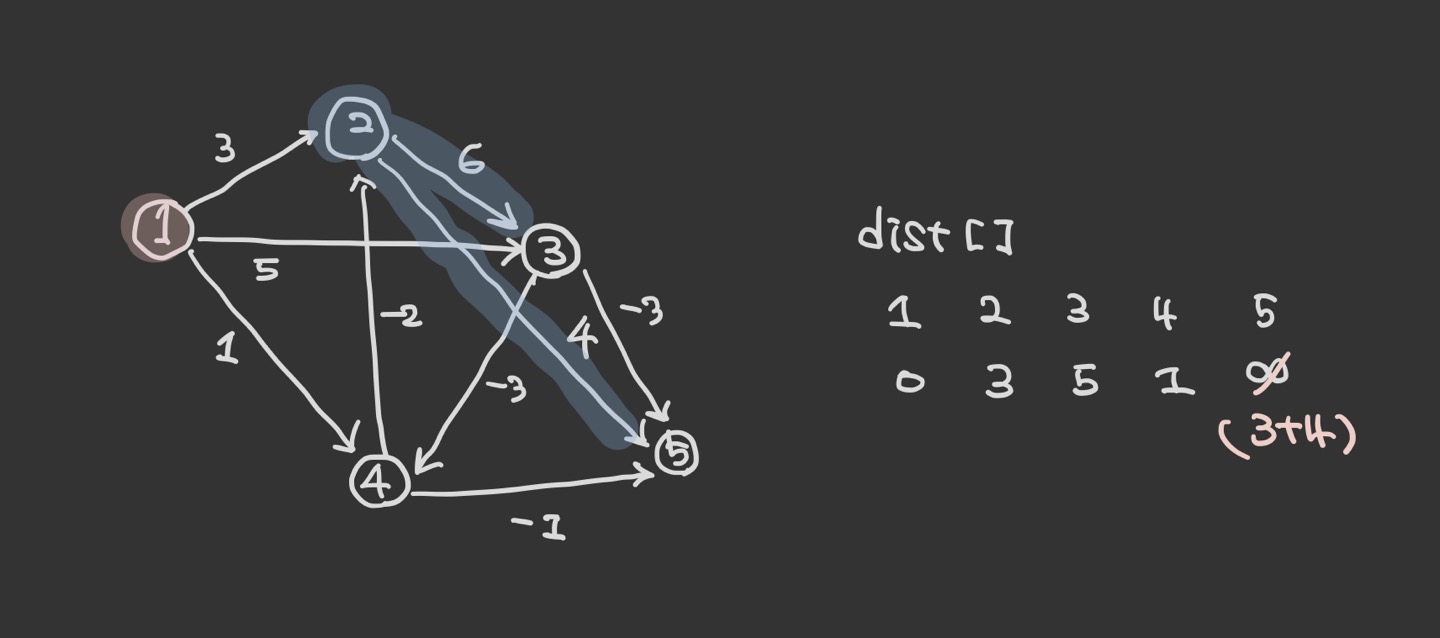
그 다음으로 2번 노드에서 나가는 간선에 의해 dist[5]가 7로 갱신되며, dist[3]은 원래 기존의 값이 갱신될 때의 값보다 작으므로 유지한다.
위 과정을 반복한다.
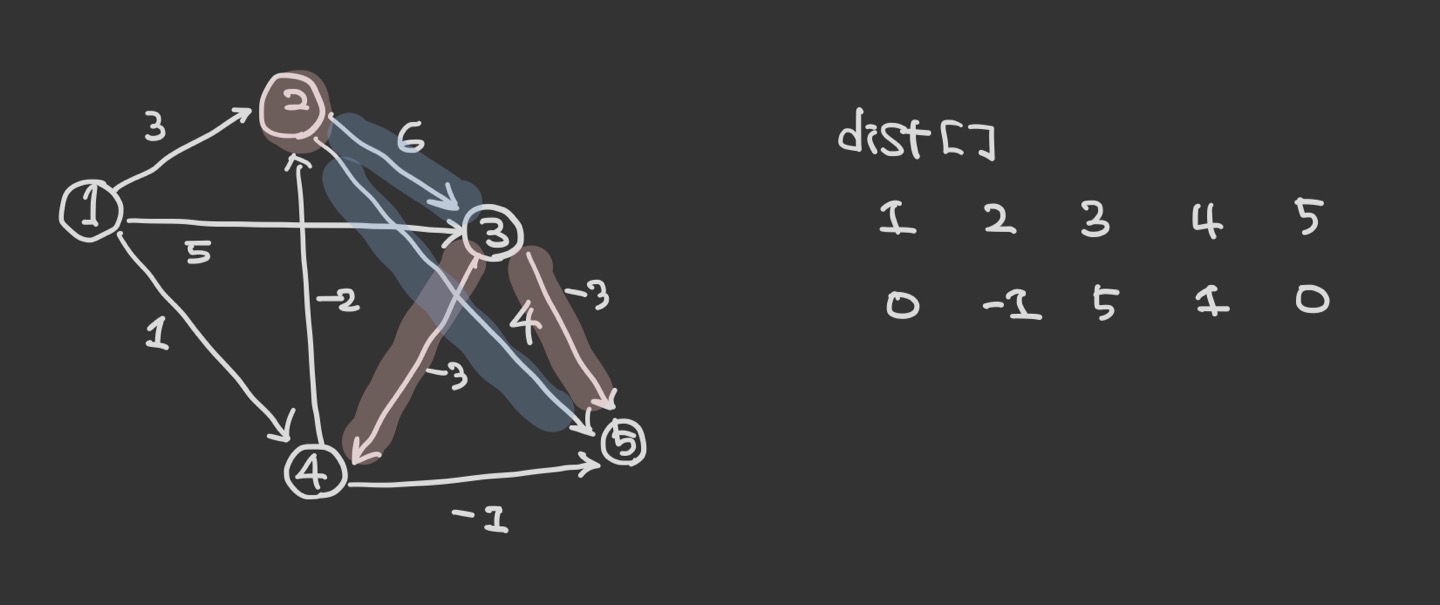
이렇게 1번 노드에 대해서는 끝난 것이다. 이후의 반복에서는 다른 노드를 순서대로 시작점으로 두로 최단 거리를 갱신하면 된다. ( 다만 지금 이 그래프에서는 갱신이 발생하지 않는다. )
이 반복은 정점의 개수 V에 대해 V-1번만 진행한다.
음의 사이클이란?
벨만 포드 알고리즘은 음의 사이클이 없는 경우에 정상적으로 작동한다.
음의 사이클은 그래프에 존재하는 사이클의 가중치 합이 음수인 경우를 말한다.
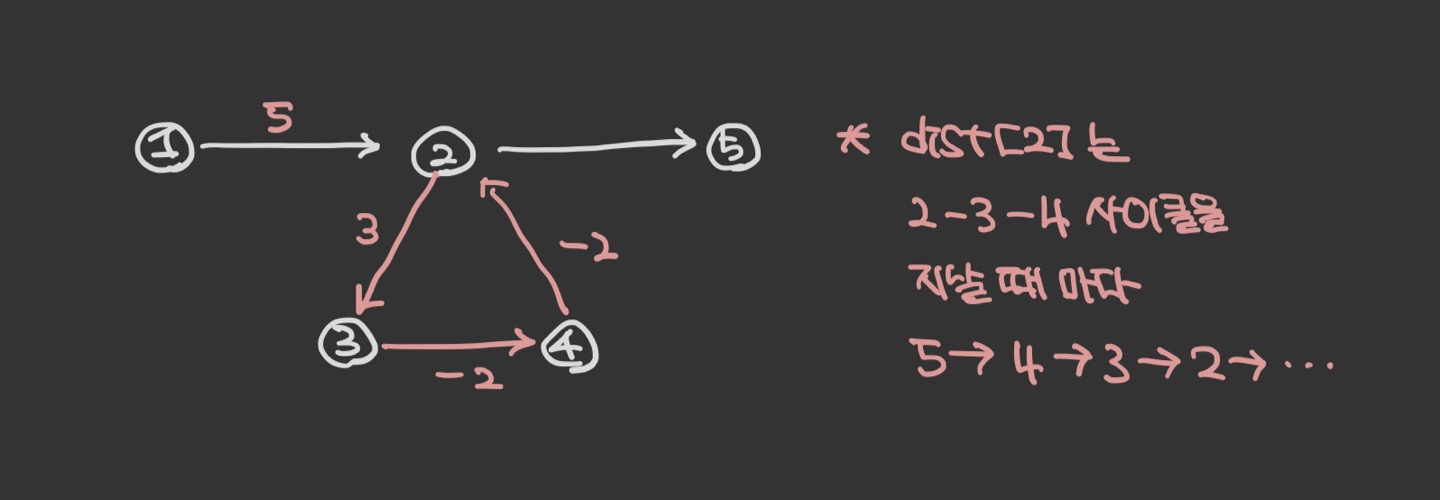
그림의 2-3-4 사이클은 한 바퀴를 돌때마다, 가중치의 합이 음수(3-2-2=-1)이 된다. 따라서 2-3-4사이클을 무한히 반복하여 지난다면, 2,3,4번 정점 모두 가중치가 음의 무한대까지 내려갈 수 있다. 이 경우 간선을 V-1개를 초과하여 지날수록 더욱 짧은 거리의 경로를 확인할 수 있다. 따라서 벨만포드 알고리즘에서는 음의 사이클을 발견한다면 최단경로가 존재하지 않는다고 결론짓는다.
음의 사이클의 존재 여부는 벨만 포드 알고리즘의 V-1번까지의 반복 이후 더 많은 반복을 하게 되는 경우 음의 사이클이 존재한다고 판단한다.
( 즉, V-1개의 간건보다 더 많은 간선을 통해 최단경로를 구할 수 있다면 음의 사이클이 존재한다고 판단한다는 것이다. )
플로이드 워셜 알고리즘 (Floyd-Warshall)
플로이드 워셜 알고리즘은 모든 노드 간의 최단 거리를 구할 수 있는 알고리즘이다. 한 노드에서 다른 모든 노드까지의 최단 거리를 수하는 다익스트라와 벨만 포드 알고리즘과 대조된다.
전체 쌍 유형을 효율적으로 해결하는데 적용할 수 있는 알고리즘이며 음수 사이클 존재 여부도 확인할 수 있어 음수 가중치를 가지는 그래프에도 적용할 수 있다.
플로이드 워셜 알고리즘도 벨만 포드와 마찬가지로 그래프 상에 음의 가중치가 있더라도 최단 경로를 구할 수 있다. 그러나 음의 가중치와 별개로 음의 사이클이 존재한다면 벨만 포드 알고리즘을 이용해야 한다.
플로이드 알고리즘은 모든 노드 간의 최단 거리를 구하고, 이때 점화식이 사용되기에 동적계획법에 해당한다. 동적 계획법에 해당하므로 최단 거리를 업데이트할 테이블이 필요하다. 이 때 모든 노드간의 최단거리이므로 2차원 배열이 사용된다. ( 특정 한 노드에서 출발하는 다익스트라가 1차원 배열을 사용하는 것과 차이점이 있다. )
플로이드 알고리즘은 각 단계마다 특정한 노드 k를 거쳐 가는 경우를 확인한다.
플로이드워셜 동작 원리
경유지 k, 출발 정점 i, 도착 정점을 j 라고 하고, 그래프는 graph라는 이중 배열에 저장되어 있다. graph[i][j]는 i번 노드에서 j번 노드까지 가는 최단 거리이다.
만약, graph[i][k]+graph[k][j]면 i부터 j까지 가는 최단거리이다.
graph[i][j]>graph[i][k] + graph[k][j]이면 i부터 j까지 가는데 k를 거쳐서 가는 것이 더 최단거리이다. 따라서 graph[i][j]는 graph[i][k]+graph[k][j]로 갱신해준다.
[도출한 플로이드-워셜 점화식]
graph[i][j] = min(graph[i][j], graph[i][k]+graph[k][j])
동작과정 살펴보기
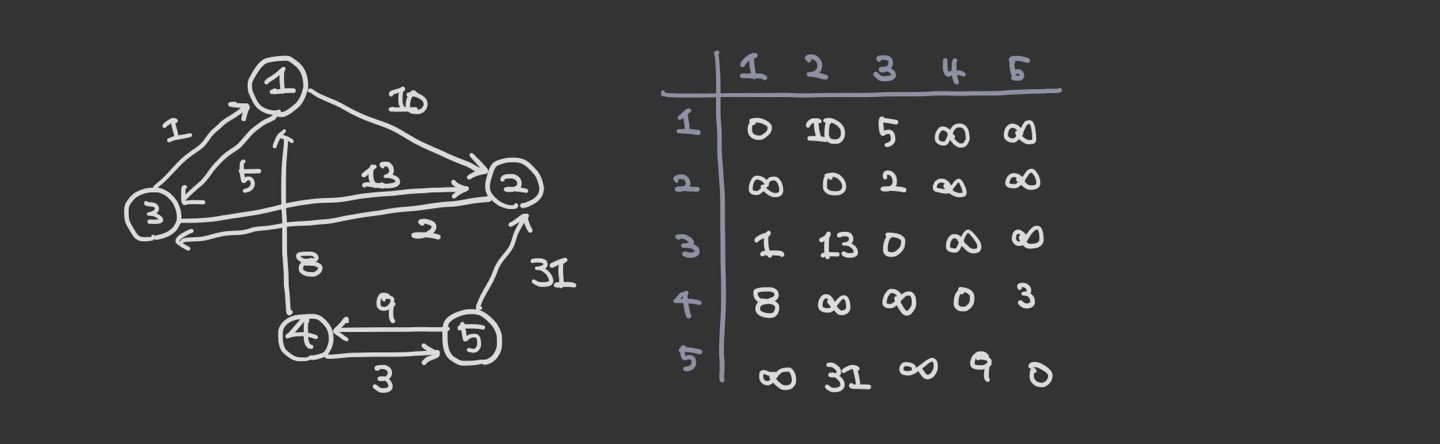
일단 2차원 배열을 선언하고 초기화한다. i와j가 같다면 0, 다른칸은 INF로 초기화 한다. 그리고 최단 거리 배열에 그래프 데이터를 저장한다. 출발 노드를 i, 도착 노드를 j라 하면 graph[i][j]=w로 에지의 정보를 배열에 입력한다. 플로이드 워셜은 모든 노드 사이의 최단 거리를 알 수 있으므로 인접 행렬로 나타낸다.
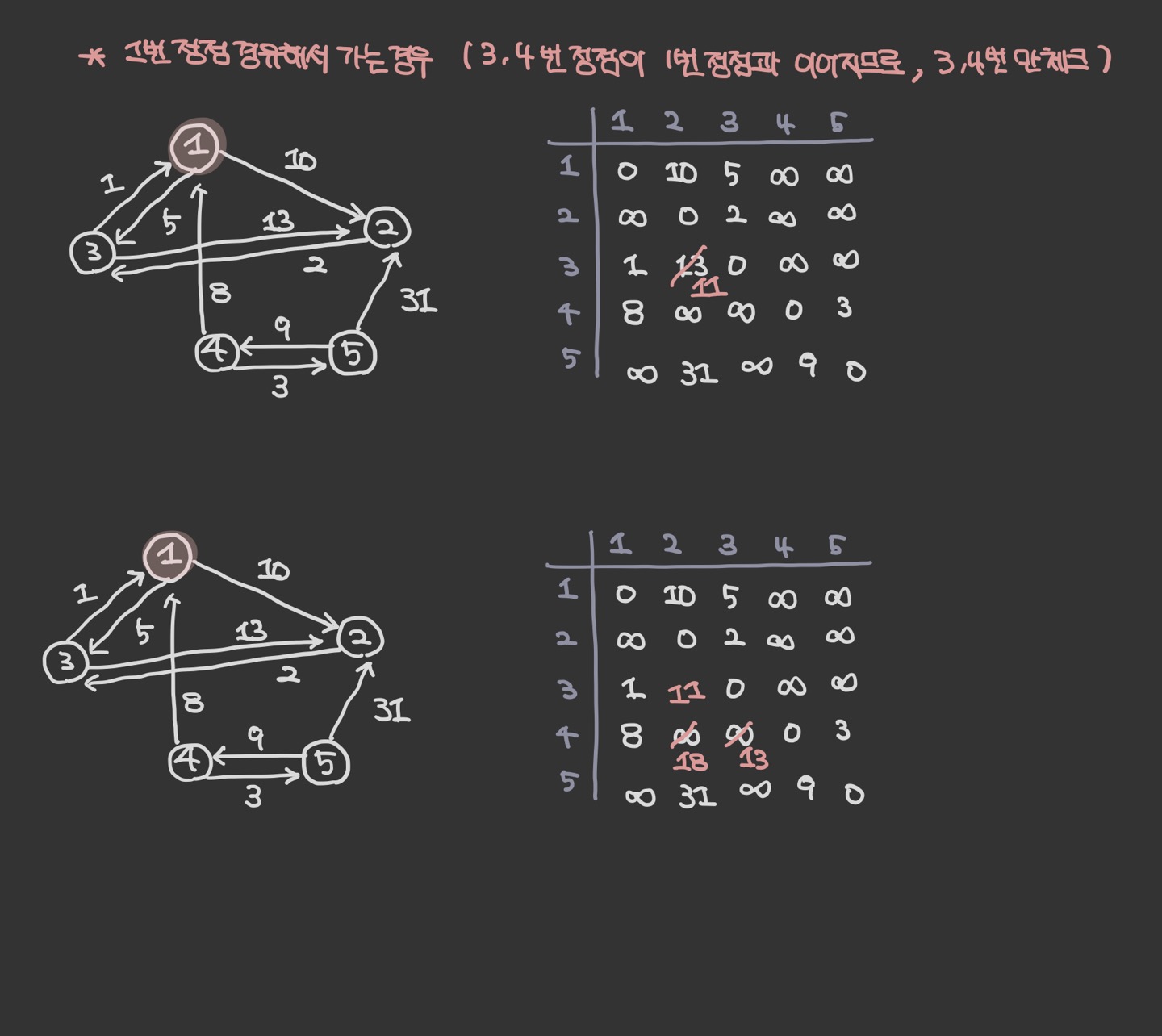 그리고 각각 정점 K번을 지날때를 생각하며 최단 거리를 갱신해준다.
그리고 각각 정점 K번을 지날때를 생각하며 최단 거리를 갱신해준다.
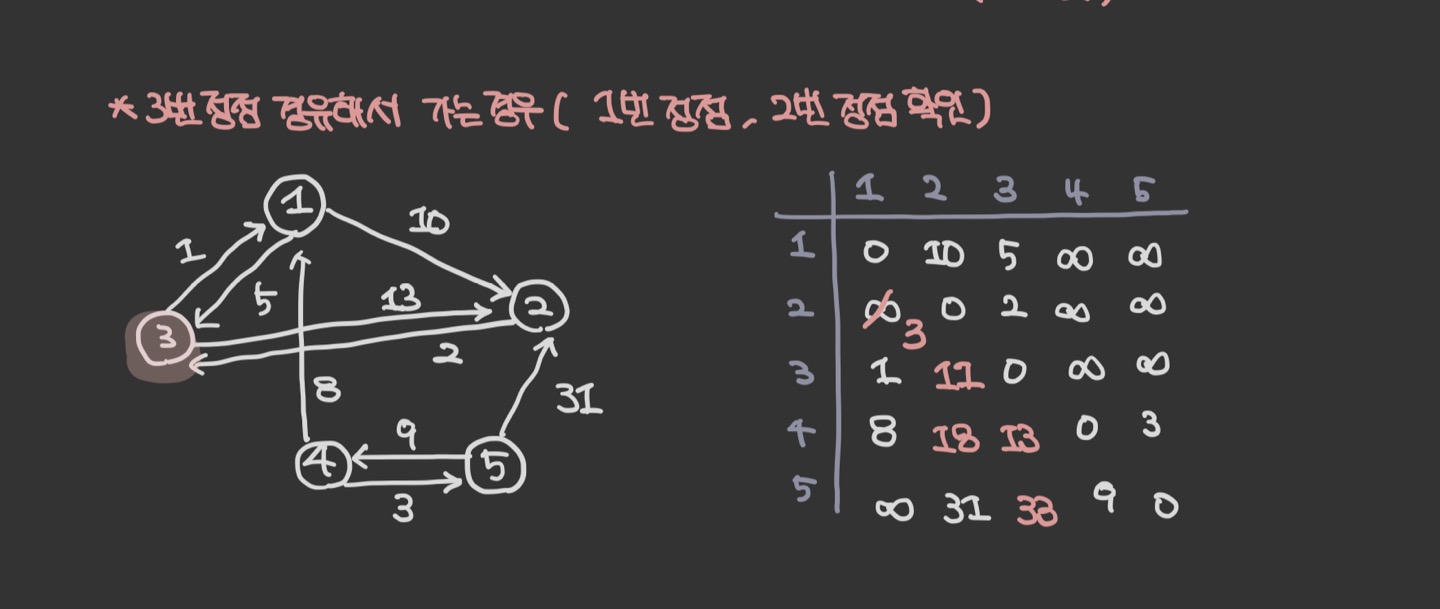
1번 정점과 이어져 있는 정점은 3번, 4번 이다.
- graph[3][2] = 11로 값을 변경해야 한다.
graph[3][2] = 13이고 graph[3][1]+graph[1][2]=1+10 = 11이기 때문이다.
- graph[4][2] = 11로 값을 변경해야 한다.
graph[4][2] = INF graph[3][1] +graph[1][2] = 8+10 = 18이기 때문이다.
- graph[4][3] = 13로 값을 변경해야 한다.
graph[4][3] = INF graph[4][1] +graph[1][3] = 8+5 = 13이기 때문이다.
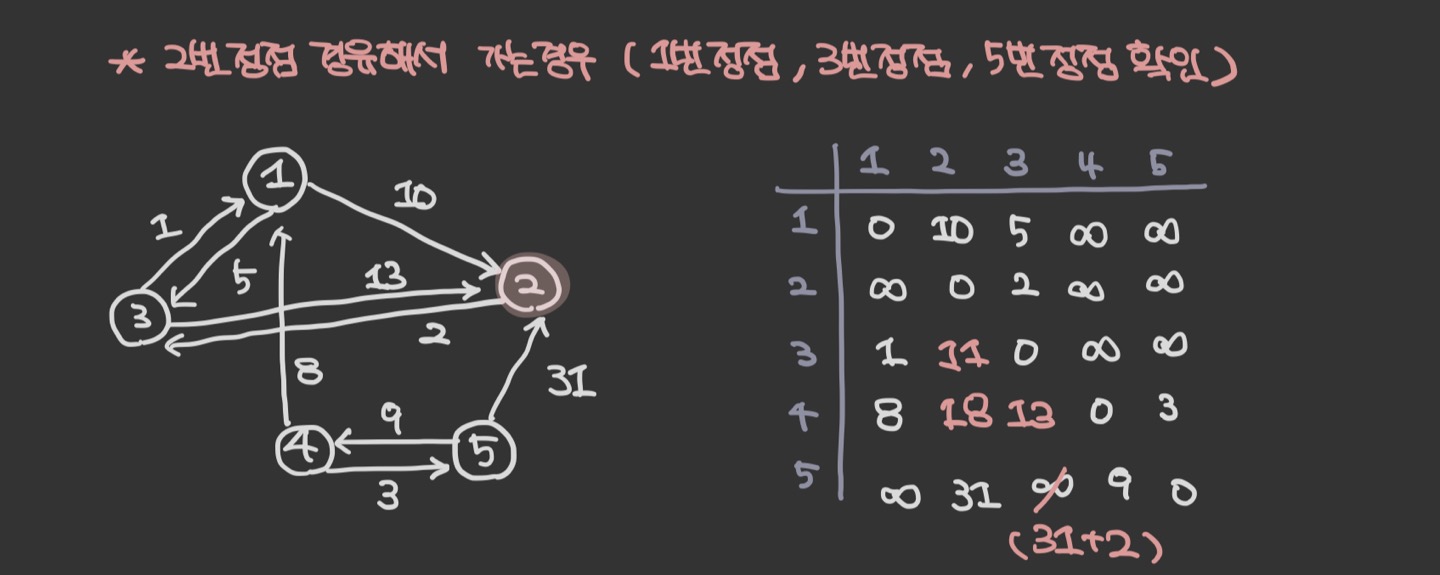
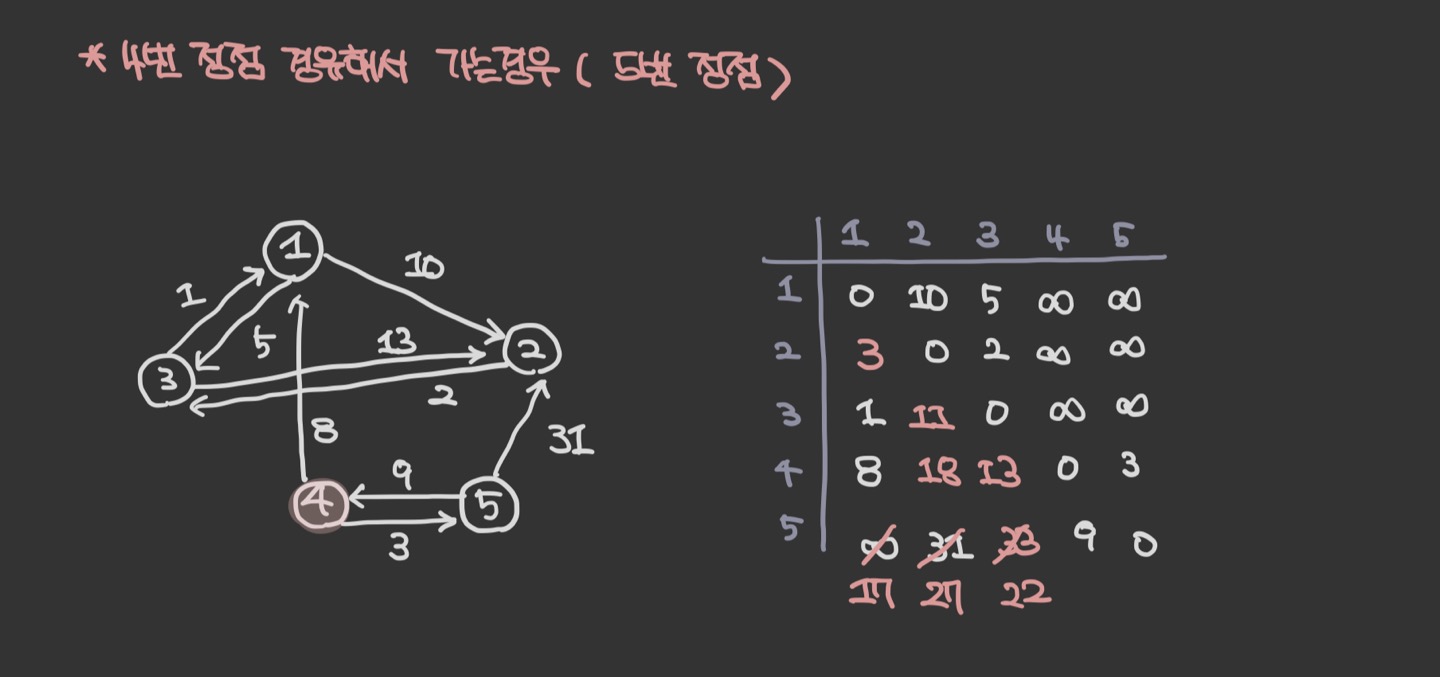
그 다음으로는 2번 정점을 경우해서 갈 경우, 3번,4번,5번 의 경우에 대해서 최단 거리를 비교해주면서 값을 갱신하면 된다.
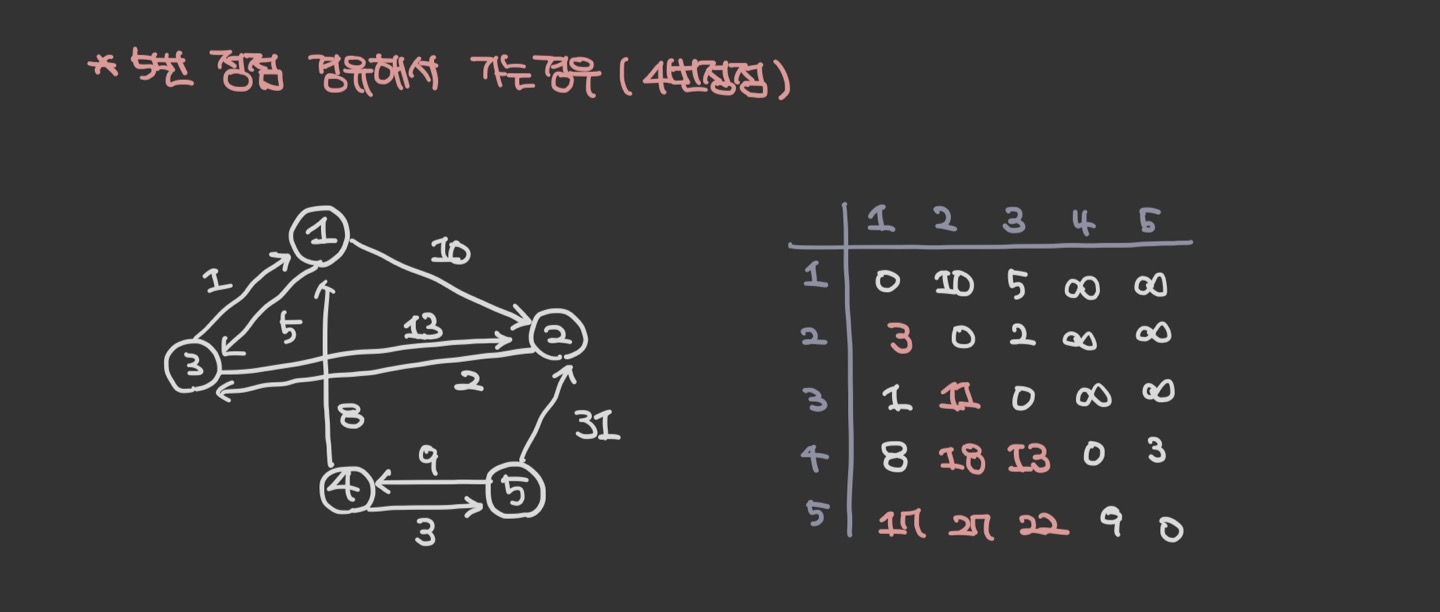
이렇게 최종적으로 완성된 2차원 배열을 볼 수 있다.
완성된 2차원 배열은 모든 노드 간의 최단 거리를 알려 준다. 예를 들어 2번에서 3번 노드 까지의 최단거리는 dist[2][3]로 나타낼 수 있음을 알 수 있다.
이처럼 플로이드 워셜알고리즘은 모든 노드 간의 최단 거리를 확인해 주기 때문에 시간 복잡도가 O(V^3)으로 빠르지 않은 편이다.
알고리즘 총 정리
처음에 최단 경로 알고리즘을 공부했을때 그 알고리즘의 특징에만 주목하여 공부하다 보니 최단 경로 알고리즘끼리 차이점을 비교해보고 싶었는데 이번에 드디어 비교하는 글을 작성하게 되었다. 스스로 정리하면서 각각 어떤 문제 상황에 적용해야 될지 알 수 있었다. 또한 에이스타 알고리즘이나 SPFA 알고리즘도 최단 경로 알고리즘으로 알고 있는데, 나중에 시간나면 이도 정리해 보아야 겠다!
Reference
- Do it! 알고리즘 코딩 테스트 자바 편 (김종관 저, 이지스퍼블리싱)
- 벨만-포드알고리즘(Bellman-Ford Algorithm, 4Legs ) *[알고리즘/Java] 플로이드-와샬(Floyd-Warshall) 알고리즘, suk13574