[Algorithm] 다익스트라 알고리즘
사실 다익스트라 알고리즘은 최단 경로 알고리즘 정리 편에서 다루었으나, 구현 방법에 대해서는 다루지 않았기 때문에 정리하면 좋을 것 같아 따로 포스트를 올리게 되었다.
다익스트라 알고리즘 (Dijkstra) 특징
특정 노드에서 출발하여 다른 모든 노드로 가는 최단 경로를 계산한다. 음의 간선이 존재하지 않을 때 이용하는 알고리즘이다. 매번 비용이 가장 최소로 들어가는 노드를 선택해 임의의 과정을 반복한다는 점에서 그리디 알고리즘이다. 단일 출발, 단일 도착, 단일 쌍 유형의 최단 경로 구하기 문제에 적용할 수 있다. 기본적으로 그리디 알고리즘이다 다이나믹 프로그래밍 기법을 사용한 알고리즘이다.
이 외에도 동작원리가 궁금하다면 최단 경로 알고리즘 “최단 경로 알고리즘 정리”을 정리해둔 글로 가면 자세한 동작 원리를 확인해 볼 수 있다.
구현 방법
다익스트라 알고리즘은 기본적으로 큐로 구현할 수 있으나, 우선순위 큐(힙)을 이용해 구현하면 더 효율적인 효과를 도출해 낼 수 있다.
큐를 이용한 방법 (O(V^2))
큐를 이용하는 방법이다. 시간 복잡도는 O(V^2) 이다. 이때 V는 노드의 개수. 각 단계마다 방문하지 않은 노드 중에서 가장 짧은 거리의 노드를 선택하기 위해 1차원 배열을 두어 모든 원소를 순차 탐색한다.
소스코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.StringTokenizer;
class node{
int index;
int cost;
//정점 번호, 가중치 저장
public node(int index, int cost){
this.index = index;
this.cost = cost;
}
}
public class DijkstraQ {
static ArrayList<node>[] graph;
static int[] dist;
static boolean[] check;
public static void dijkstra(int n, int start){
//방문 여부를 저장할 배열 생성
check = new boolean[n+1];
dist = new int[n+1];
int INF = Integer.MAX_VALUE;
Arrays.fill(dist,INF); //거리 배열 초기화 (fill() 메소드를 이용해 전체 초기화)
dist[start]=0; //그리고 시작점을 0으로 초기화 한다.
//다익스트라 알고리즘 실행. 모든 노드를 방문하면 종료되기 때문에 노드의 개수만큼 반복
for(int i=0;i<n;i++){
//순차 탐색을 통해 dist 값이 가장 작은 노드를 선택한다.
int nodeIdx = getSmallNode(n);
check[nodeIdx]=true;
//인접 노드 처리 (현재 노드를 거쳐서 도착하는 값이 dist테이블에 저장된 값보다 작을경우 값을 갱신)
for(node next: graph[nodeIdx]){
if(dist[next.index]>dist[nodeIdx]+next.cost)
dist[next.index] = dist[nodeIdx]+next.cost;
}
}
//최소 거리 출력
for(int i: dist){
if(i==INF) System.out.print("INF ");
else System.out.print(i+" ");
}
}
public static int getSmallNode(int n){
// 방문하지 않았고, dist 값이 최소인 노드를 순차탐색후 index 번호 반환
// priorityqueue를 사용하지 않았기에 순차탐색으로 하나하나 비교하여 확인한다.
// 이 코드 때문에 시간복잡도가 O(V^2)가 되는 것이다.
int min = dist[0];
int index =0;
for(int i=1;i<n+1; i++){
if(dist[i]<min && !check[i]){
min = dist[i];
index=i;
}
System.out.println(Arrays.toString(dist));
}
System.out.println("선택 노드 : "+index);
return index;
}
public static void main(String[]args)throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
System.out.print("정점의 개수와 간선 개수 입력 (예 : 3 4 ) >>");
st = new StringTokenizer(br.readLine());
int n =Integer.parseInt(st.nextToken()); //정점 개수
int m = Integer.parseInt(st.nextToken()); //간선 개수
//graph 정의
graph = new ArrayList[n+1];
for(int i=0;i<n+1;i++) graph[i] = new ArrayList<>();
//시작 노드, 도착노드, 가중치 입력
System.out.println("시작노드, 도착노드,가중치 입력 (예 :1 3 10 ) >>");
for(int i=0;i<m;i++){
st = new StringTokenizer(br.readLine());
int v = Integer.parseInt(st.nextToken());
int w = Integer.parseInt(st.nextToken());
int cost = Integer.parseInt(st.nextToken());
graph[v].add(new node(w,cost));
}
System.out.print("시작 노드 입력 >>");
int start = Integer.parseInt(br.readLine());
//다익스트라 실행
dijkstra(n,start);
}
}
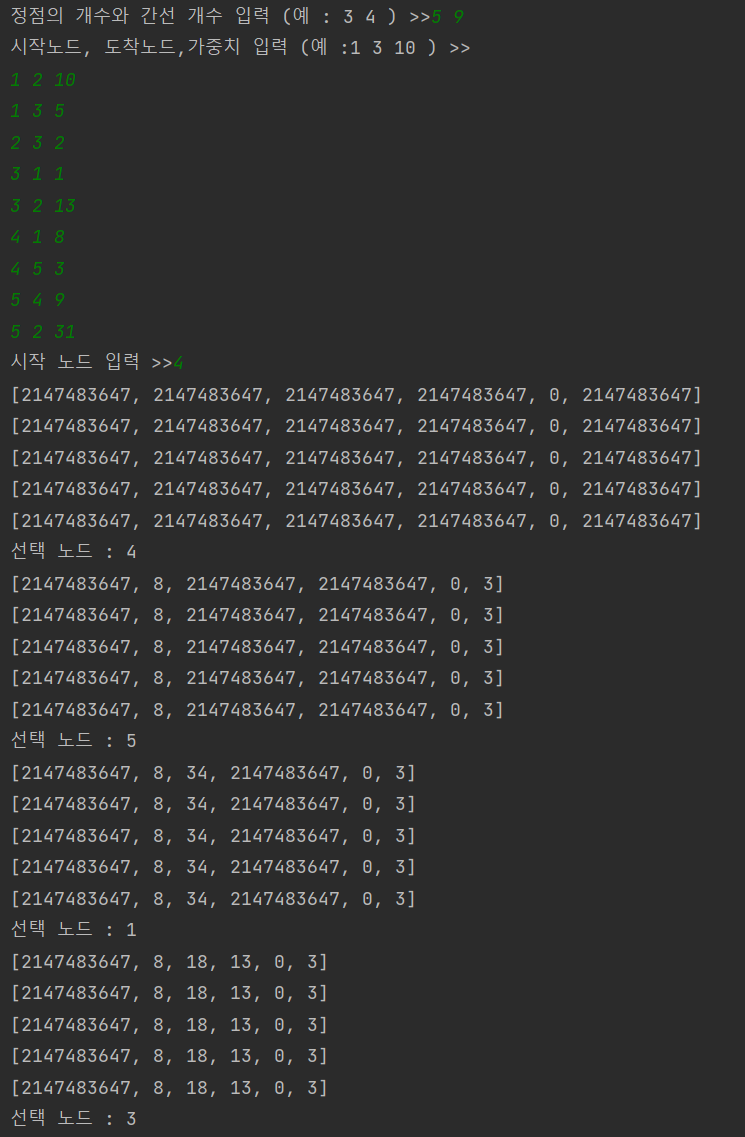
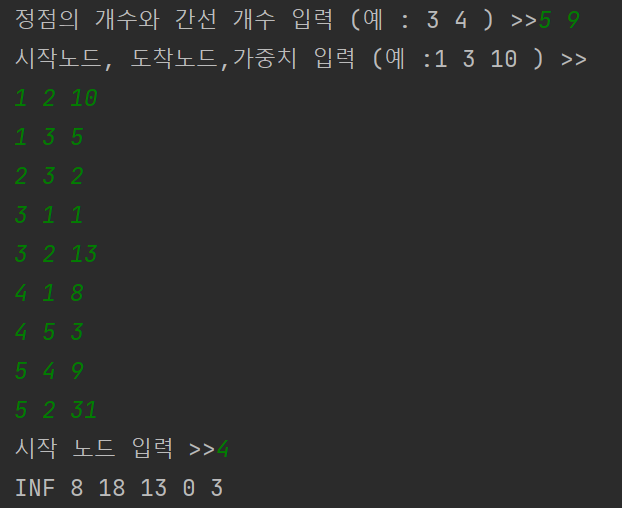
실행화면은 다음과 같다. 실제로 배열의 0번은 사용하지 않았으므로 (노드 번호는 1번부터 시작) dist 배열의 0번은 INF 값이 들어간 것을 확인할 수 있다. 또한 매번 최소 distance 값을 가진 노드를 선택하기위해 노드의 개수만큼 순차 탐색을 하는 것을 확인할 수 있다.
개선된 구현 방법 : 우선순위 큐 이용한 방법 (O(Elog V))
개선된 다익스트라 알고리즘 구현을 위해 인접 리스트 그래프 + 우선순위 큐를 사용하였다. 우선순위 큐는 배열, 인접 리스트, 힙 등으로 구현이 가능하다. 이 중에서 힙으로 구현하는 것이 가장 효율적이다.
이때, 힙은 완전 이진 트리의 일종으로, 우선 순위 큐를 구현하는데 사용된다. 여러개의 값들 중에서 최댓값이나 최솟값을 가장 빠르게 찾을 수 있도록 만들어진 자료구조이다.
동작 원리
다익스트라 알고리즘이 동작하는 기본 원리는 동일하다.
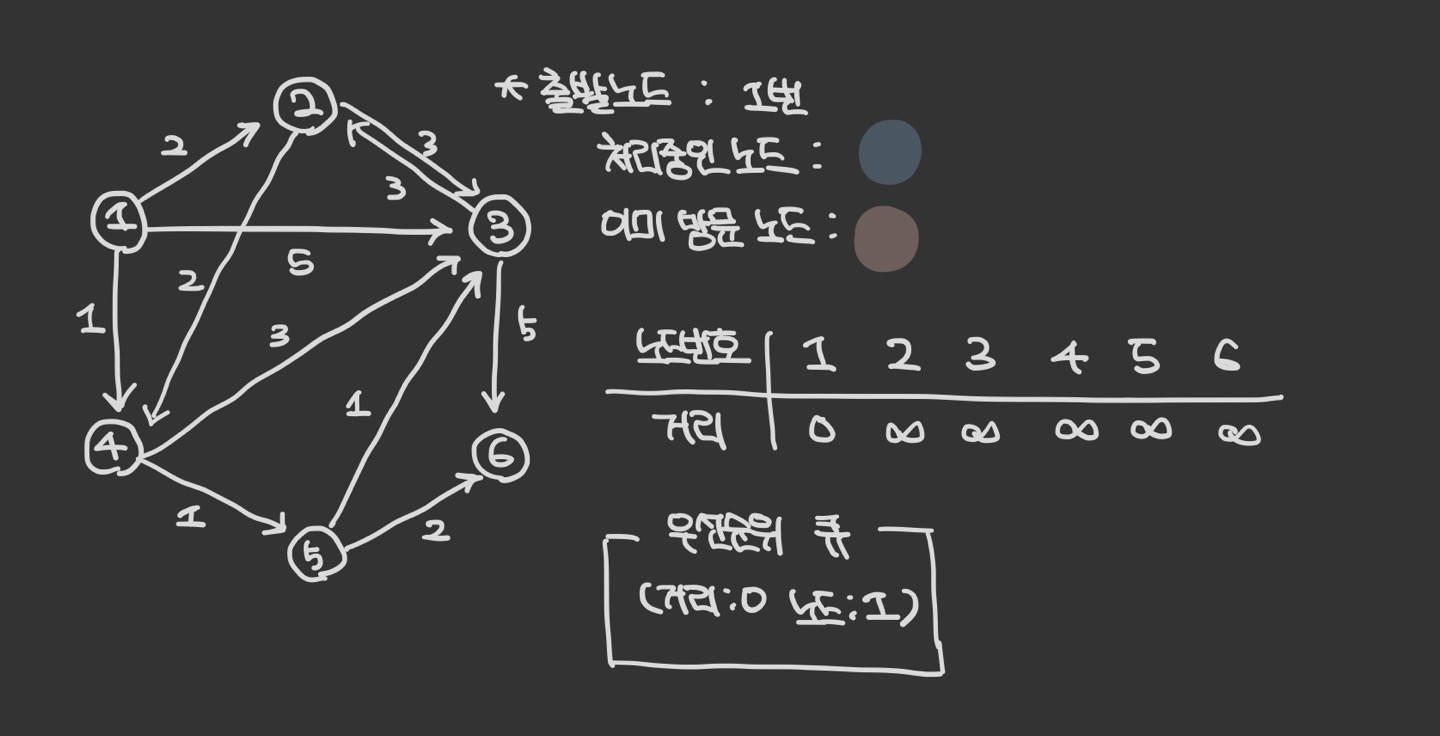
- 그래프를 준비하고 출발 노드를 설정하여 우선순위 큐를 사용한다. 또한 그림에는 visited 배열을 선언하지 않았지만, visited 배열을 구현해 방문 여부를 판단할 수 있다.
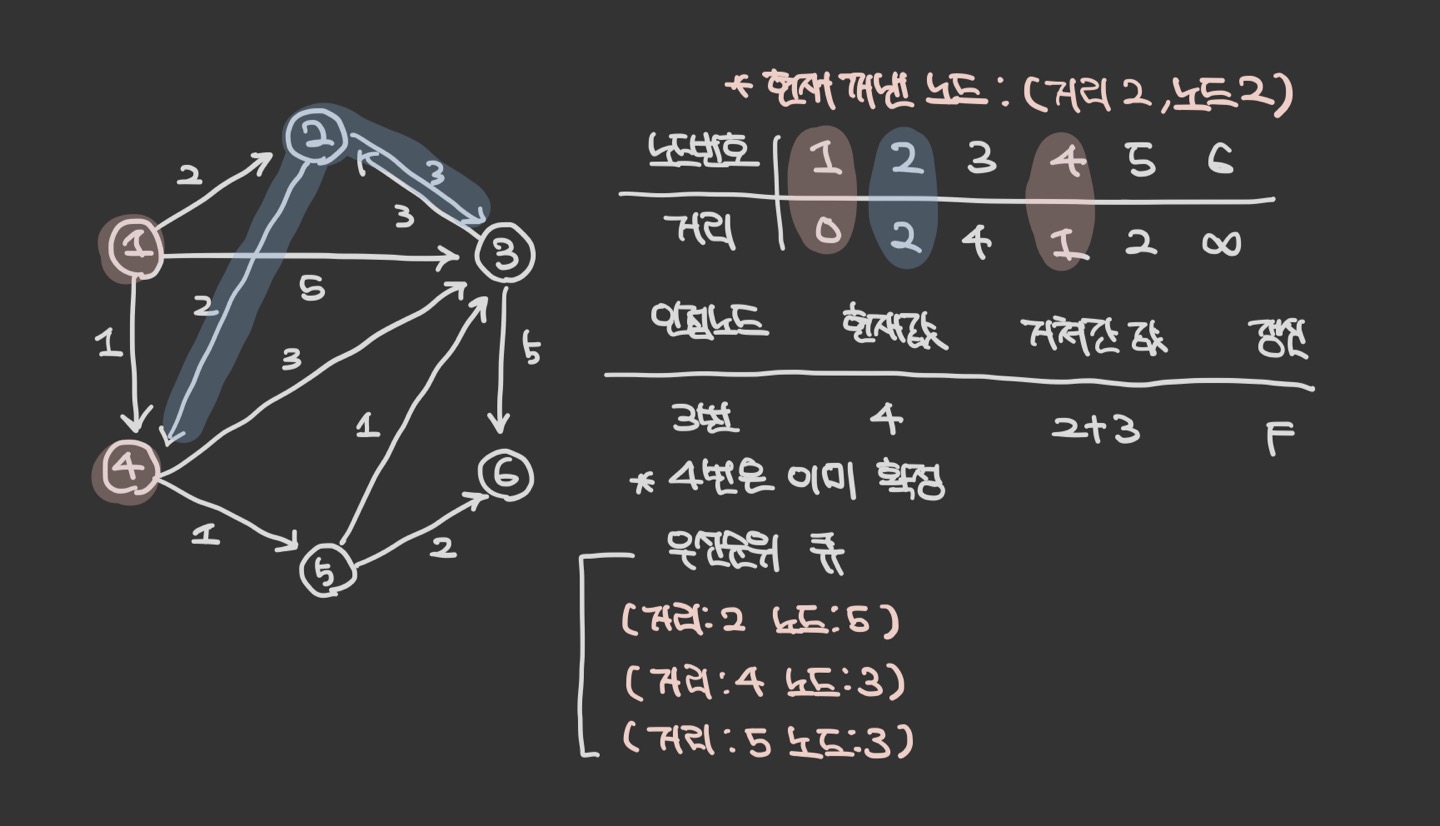
그래프를 준비하고 출발 노드를 설정하여 우선 순위 큐에 삽입한다.
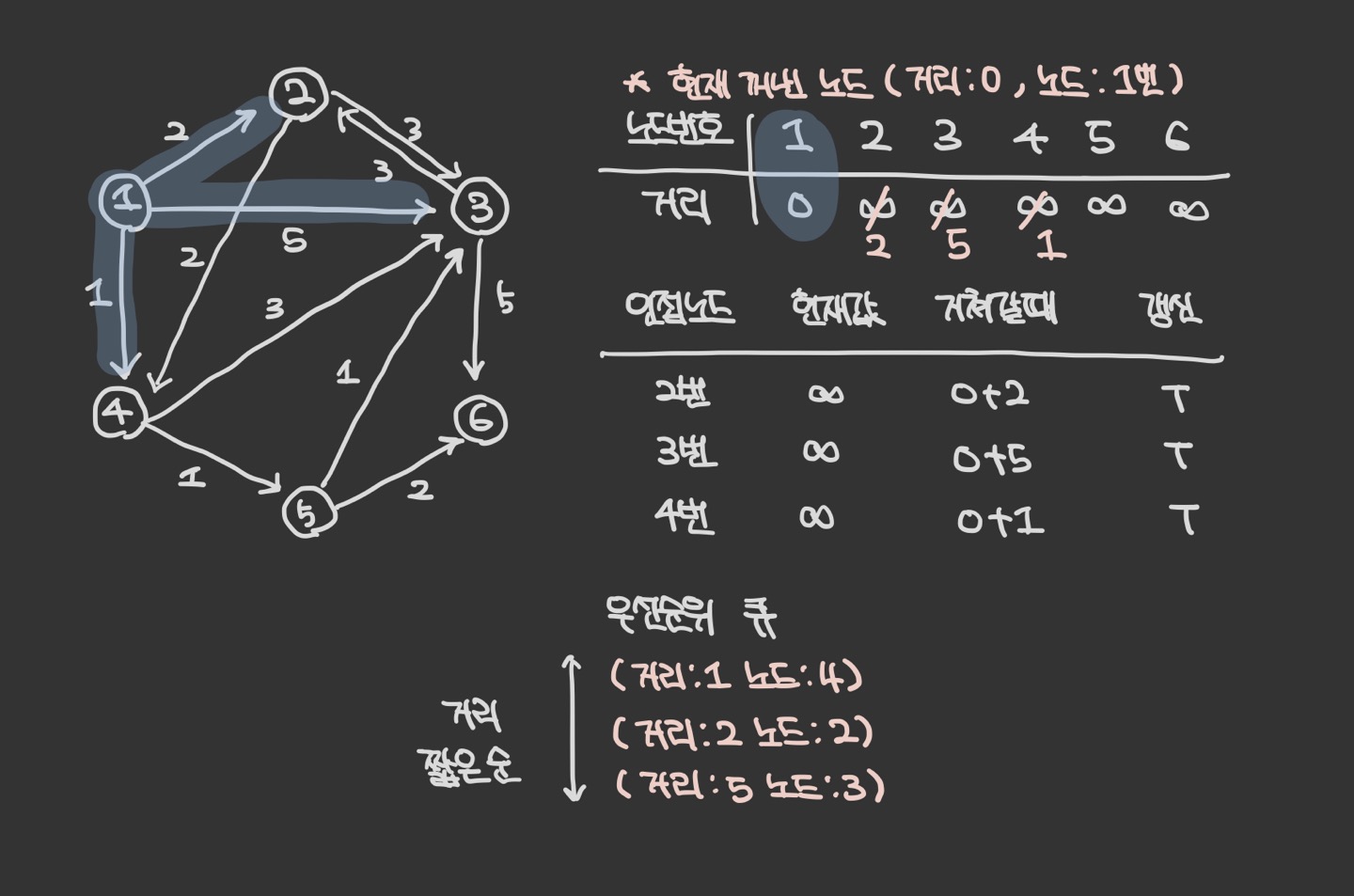
우선 순위 큐에서 원소를 꺼낸다. 1번은 아직 방문하지 않았으므로, 방문 처리한다. ( 방문 여부는 visited 배열을 생성하거나, 테이블의 거리 값과 큐에서 꺼낸 원소의 거리 값을 비교하면 된다. )
- 1번 노드에서 이동할 수 있는 ( 방문하지 않은 인접 노드 ) : 2, 3, 4번 노드
- 현재 테이블에 저장된 값보다 1번 노드를 거쳐서 가는 경로가 더 짧으면 값을 갱신하여 우선 순위 큐에 삽입한다.
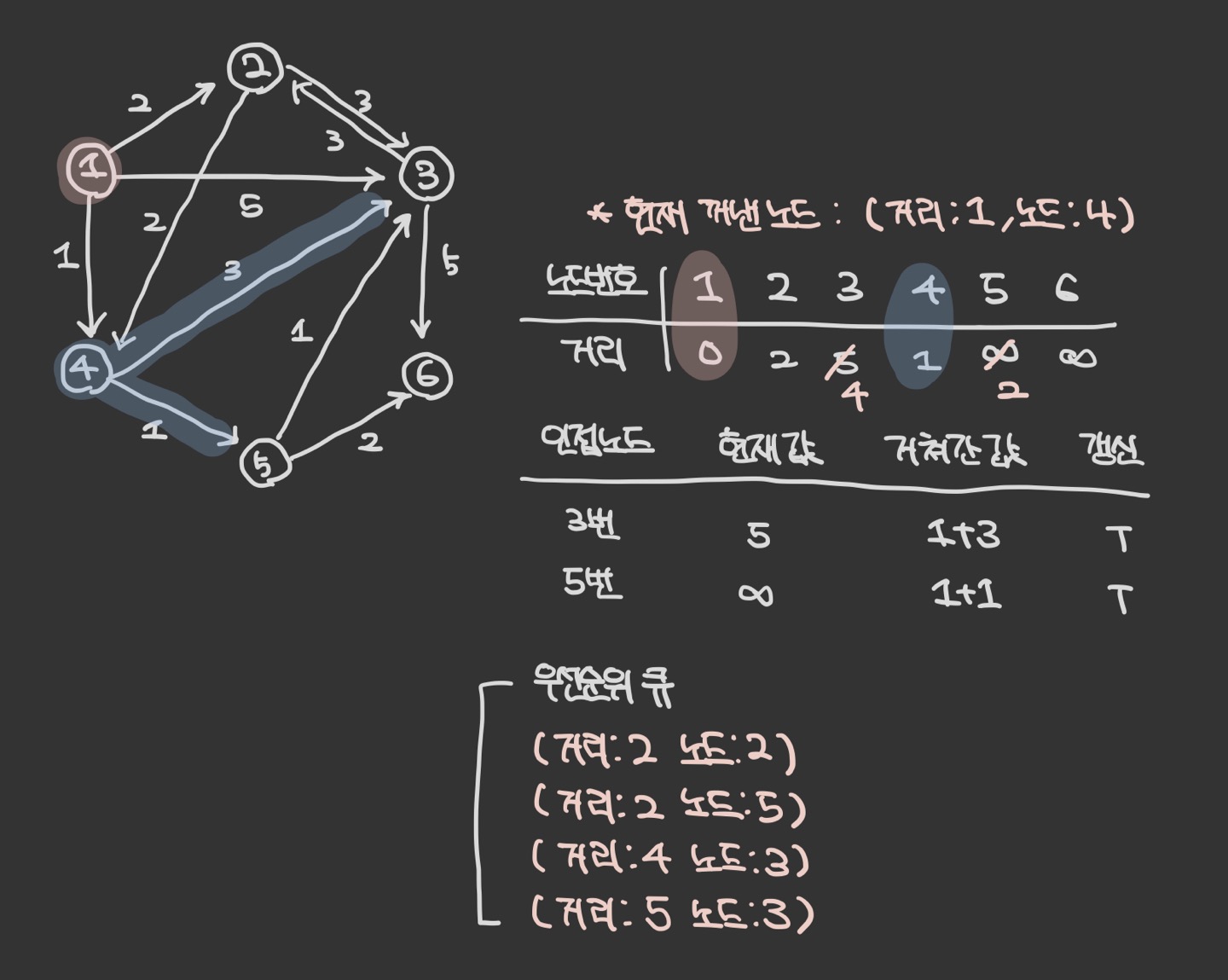
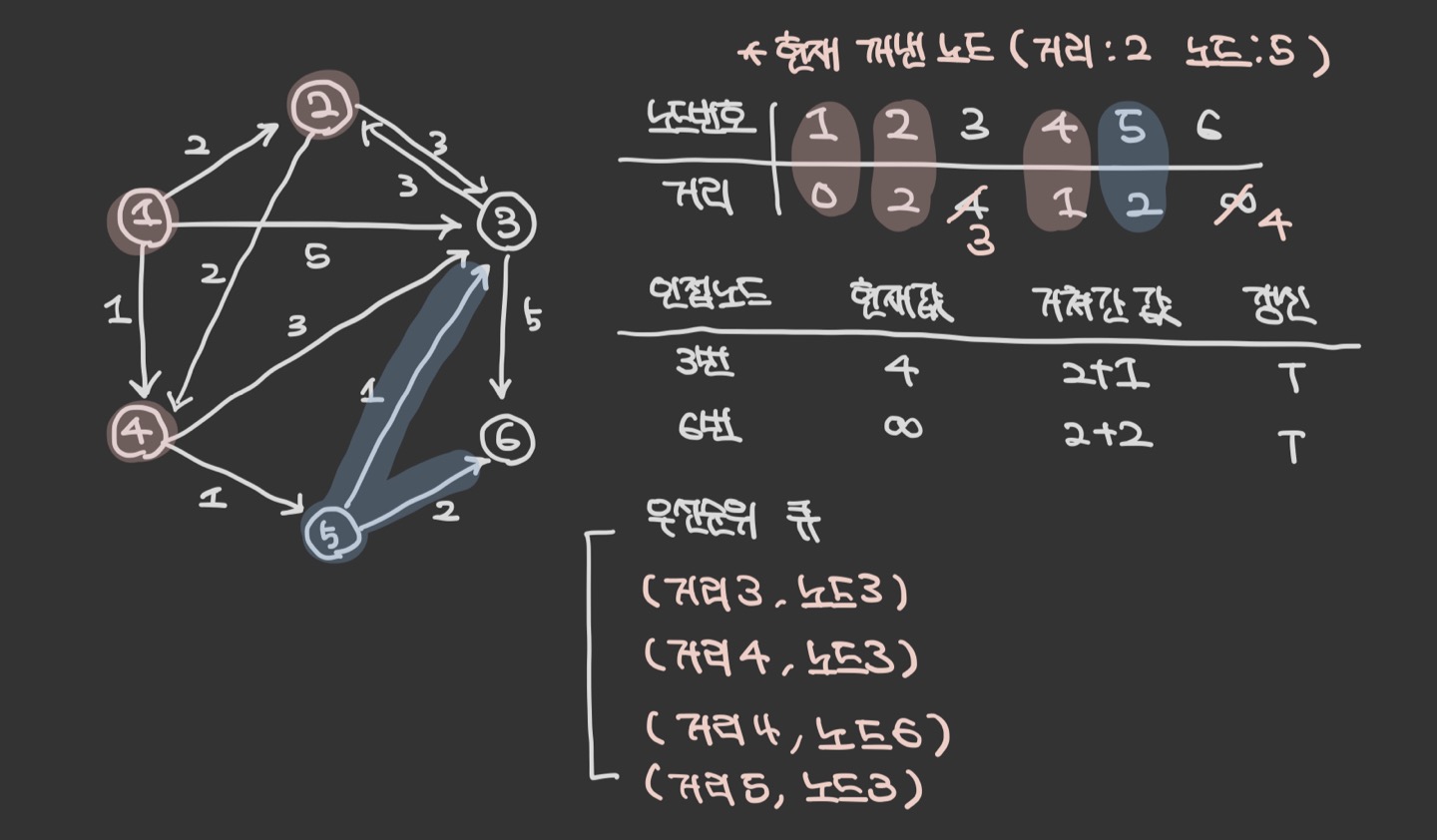
우선 순위 큐에서 원소를 꺼낸다. 4번 노드는 아직 방문하지 않았으므로 방문 처리한다. 4번에서 이동할 수 있는, 방문하지 않은 인접 노드 : 3,5 번
현재 테이블에 저장된 값보다 4번 노드를 거쳐서 가는 경로가 더 짧으면 값을 갱신하여 우선순위 큐에 삽입한다.
이 과정을 여러번 반복하면 된다.
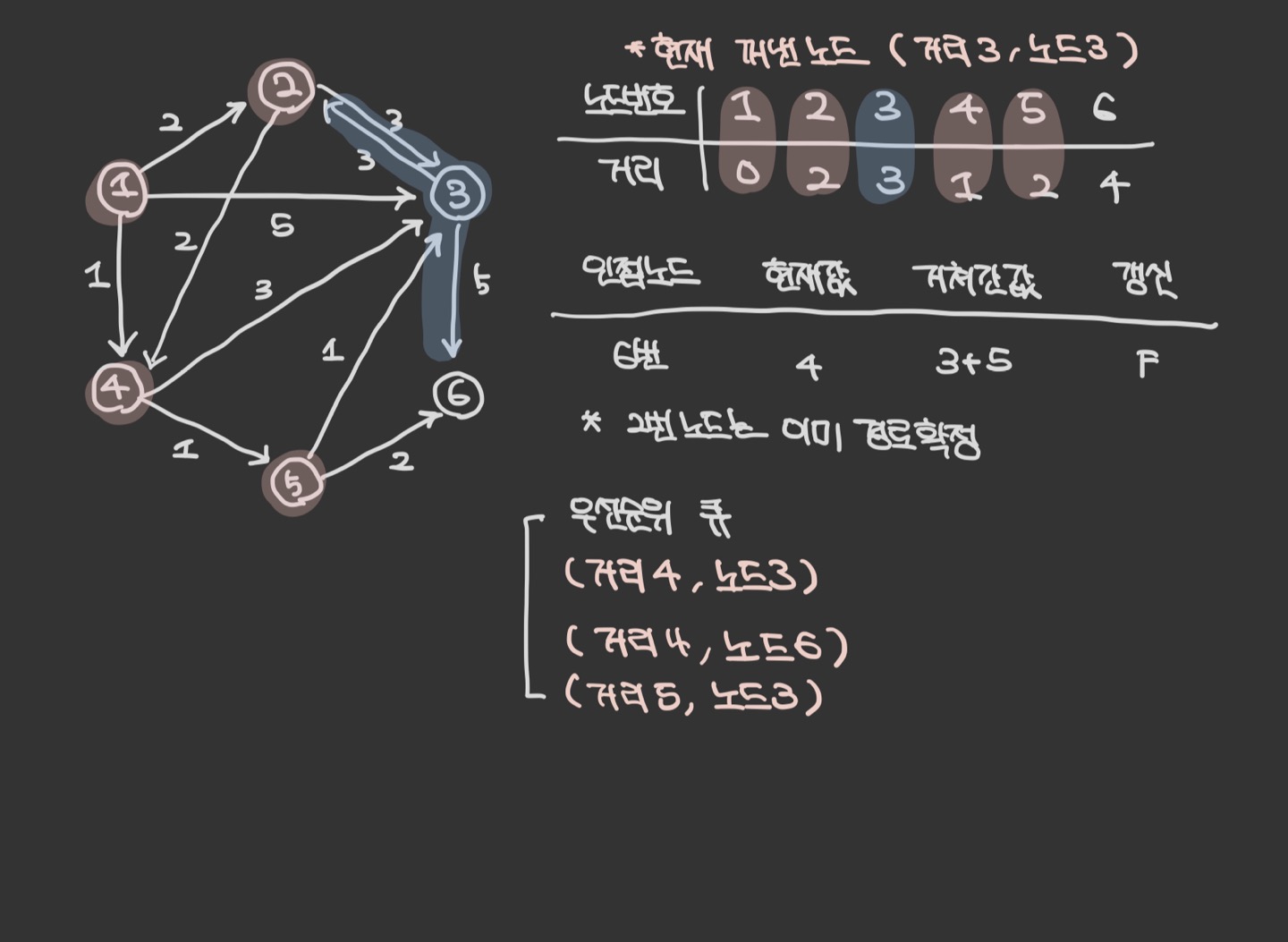
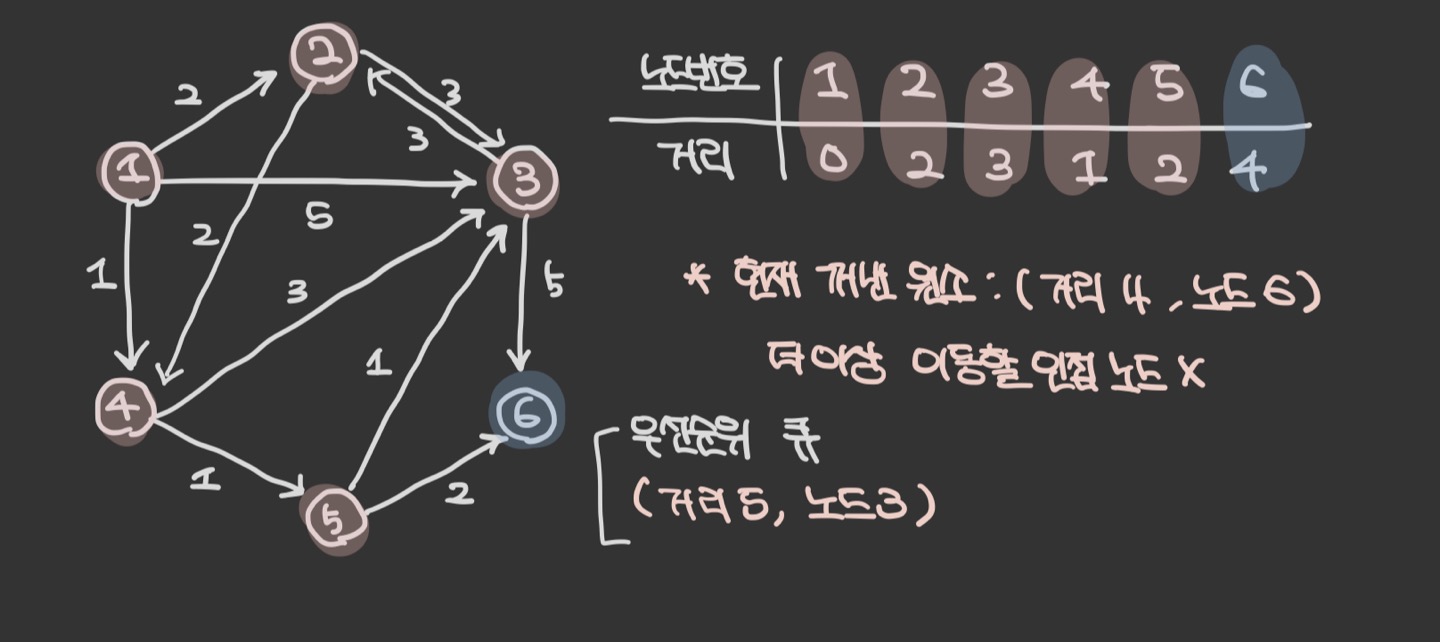
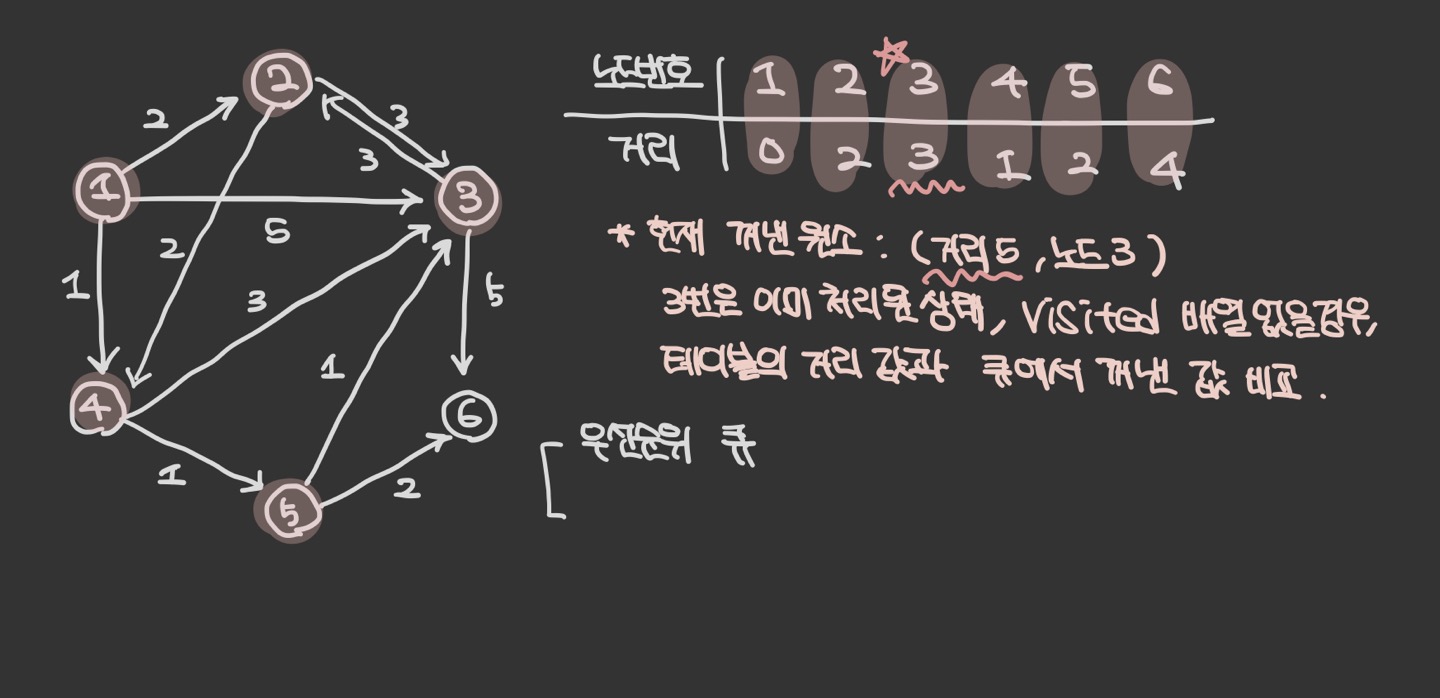
우선 순위 큐에서 원소를 꺼낸다. 이때 3번 노드는 이미 방문 처리가 된 노드이므로 패스한다.
visited 배열이 있다면, 방문했는지의 여부를 바로 판단할 수 있다.
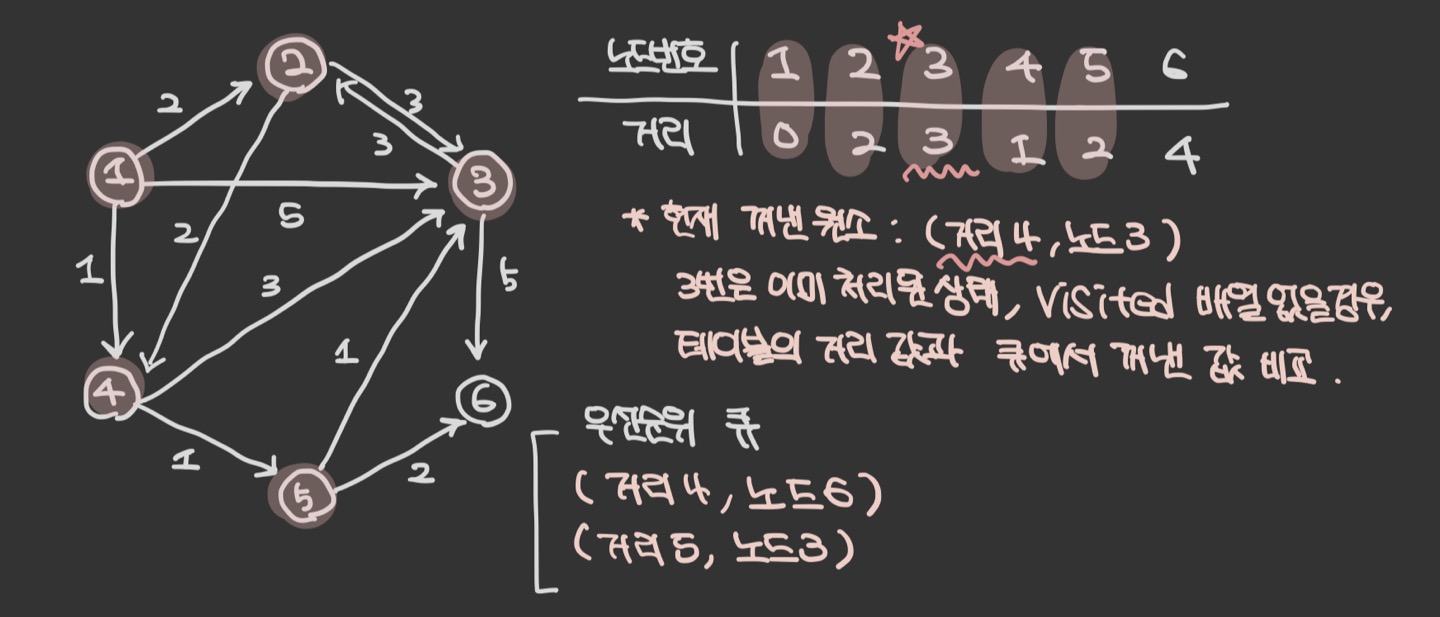
만약 없다면, 현재 3번 노드의 최단거리 테이블에 저장된 거리 값과 우선순위 큐에서 꺼낸 거리 값을 비옇여 방문 여부를 파악한다. ( 테이블에 저장된 값이 더 작다면 방문 처리 되었다고 간주 )
6번 노드는 더이상 이동할 수 있는 인접 노드가 존재하지 않는다.
소스코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.PriorityQueue;
import java.util.StringTokenizer;
public class Main {
static ArrayList<Node>[] graph;
public static void Dijkstra(int n, int start){
//방문 여부를 저장할 배열 생성
boolean[] check = new boolean[n+1];
int[] dist = new int[n+1];
int INF = Integer.MAX_VALUE;
Arrays.fill(dist,INF); //거리 배열 초기화 (fill() 메소드를 이용해 전체 초기화)
dist[start]=0; //그리고 시작점을 0으로 초기화 한다.
PriorityQueue<Node> pq = new PriorityQueue<>();
pq.offer(new Node(start,0)); //우선순위 큐 생성하고 출발노드를 삽입한다.
while(!pq.isEmpty()){
int nowVertex = pq.poll().index;
if(check[nowVertex]) continue; //만약 방문했던 노드라면 그냥 패스
check[nowVertex] = true; //아직 방문하지 않았다면 방문했다고 처리하기
//index와 연결된 인접 노드들 건사
for(Node next:graph[nowVertex]){
//만약 현재 노드를 거쳐서 도착하는 것이 현재 dist 테이블에 저장된 값보다 작다면, 값을 갱신 후 우선순위 큐에 삽입
if(dist[next.index]>dist[nowVertex]+next.cost){
dist[next.index] = dist[nowVertex]+next.cost;
pq.offer(new Node(next.index, dist[next.index]));
}
}
}
//최소 거리 출력
for(int i: dist){
if(i==INF) System.out.print("INF ");
else System.out.print(i+" ");
}
}
public static void main(String[]args)throws IOException {
//그래프 입력
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
System.out.print("정점의 개수와 간선 개수 입력 (예 : 3 4 ) >>");
StringTokenizer st = new StringTokenizer(br.readLine());
int n =Integer.parseInt(st.nextToken()); //정점 개수
int m = Integer.parseInt(st.nextToken()); //간선 개수
//graph 정의
graph = new ArrayList[n+1];
for(int i=0;i<n+1;i++) graph[i] = new ArrayList<>();
//시작 노드, 도착노드, 가중치 입력
System.out.println("시작노드, 도착노드,가중치 입력 (예 :1 3 10 ) >>");
for(int i=0;i<m;i++){
st = new StringTokenizer(br.readLine());
int v = Integer.parseInt(st.nextToken());
int w = Integer.parseInt(st.nextToken());
int cost = Integer.parseInt(st.nextToken());
graph[v].add(new Node(w,cost));
}
System.out.print("시작 노드 입력 >>");
int start = Integer.parseInt(br.readLine());
//다익스트라 실행
Dijkstra(n,start);
}
}
//Node 클래스 생성 (이 클래스는 우선순위 큐에 정점번호 + 가중치 저장을 위해 생성
class Node implements Comparable<Node>{
int index;
int cost;
//정점 번호, 가중치 저장
public Node(int index, int cost){
this.index = index;
this.cost = cost;
}
//cost 중심으로 우선순위기 저장되기 때문에 compareTo 오버라이딩 아니면 자바에 내장된 우선순위 큐를 사용해도 된다.
//PriorityQueue<Node> queue = new PriorityQueue<Node>
// ((o1,o2)->Integer.compare(o1.cost, o2.cost));
@Override
public int compareTo(Node o) {
return Integer.compare(this.cost,o.cost);
}
}
Reference
- Do it! 알고리즘 코딩 테스트 자바 편 (김종관 저, 이지스퍼블리싱)